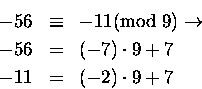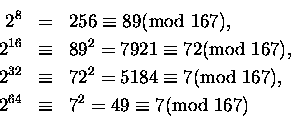Next: "Nie samą matematyką ..."
Up: Carl Friedrich Gauss
Previous: Carl Friedrich Gauss
,,Matematyka to królowa nauk, a teoria liczb to królowa Matematyki''.
Jeżeli nawet Gauss nie był autorem tego powiedzenia, to było ono z pewnością
mottem numer 1. (były i inne) jego twórczego życia.
Teoria liczb fascynowała i fascynuje matematyków od najdawniejszych czasów.
Mistyczne skojarzenia Pitagorejczyków, zażarte poszukiwania liczb doskonałych
(ojciec Mersenne), małe i wielkie twierdzenie Fermat'a - to tylko kilka z
nieprzebranej różnorodności problemów. teoria liczb jest na swój sposób łatwa i
trudna: łatwa, bo można do niej ,,wystartować'' bez specjalnego przygotowanie
formalnego, trudna - bo niektóre oczywiste (?) przypuszczenia opierają się przez
setki lat rygorystycznym dowodom.
Niekiedy rzeczy ,,trudne'' stają się dziecinnie łatwe - jeżeli tylko pojawi się sprytna
metoda uwidaczniania (i udowadniania) pewnych własności. Taką metodą jest
właśnie teoria kongruencji, albo przystawania liczb. Nie jest ona
wyłącznie dziełem Gaussa, ale została przez niego dopracowana, skodyfikowana i
...wykorzystana do rozstrzygnięcia wielu pytań związanych z podzielnością
liczb.
Definicja:
Niech n będzie dodatnią liczbą całkowitą, natomiast a i b - dowolnymi
liczbami (całkowitymi - rozmawiamy wyłącznie o liczbach
całkowitych). Liczby a i b nazywamy przystającymi (kongruentnymi)
modulo n i piszemy
jeżeli różnica a - b jest podzielna przez n:
Na przykład:
bo mamy:
Analogicznie, możemy mówić o liczbach, które nie są przystające modulo n
i pisać
Na przykład:
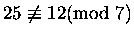 ,
bo
25-12 = 13 - liczbie, która nie
jest podzielna przez 7.
Z definicji natychmiast wynika oczywiste twierdzenie: warunkiem koniecznym i
wystarczającym aby
,
bo
25-12 = 13 - liczbie, która nie
jest podzielna przez 7.
Z definicji natychmiast wynika oczywiste twierdzenie: warunkiem koniecznym i
wystarczającym aby
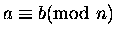 jest aby reszty z dzielenia a i b
przez n były równe. Dowód (w obie strony )jest banalnie prosty. Ale i tak
zachęcam do spróbowania.
Na przykład:
jest aby reszty z dzielenia a i b
przez n były równe. Dowód (w obie strony )jest banalnie prosty. Ale i tak
zachęcam do spróbowania.
Na przykład:
- reszta w obu przypadkach wynosi 7.
Kongruencja albo (po polsku) przystawanie liczb całkowitych okazuje
się mieć podobne własności w stosunku do operacji dodawania, mnożenia i
potęgowania jak zwykła relacja równości.
Podstawowe własności kongruencji to:
- 1.
-
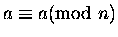 ;
;
- 2.
-
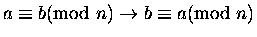
- 3.
-
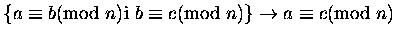 ;
;
- 4.
-
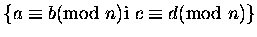
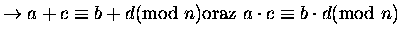
- 5.
-
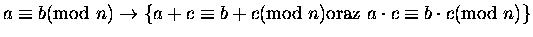 ;
;
- 6.
-
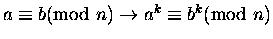
I znowu dowody powyższych własności są bardzo proste. Jeżeli chcesz się
naprawdę nacieszyć następnymi przykładami i zadaniami to radzę - udowodnij
sam(a). Jeżeli jesteś leniuszek, to - proszę - choć, prawdę mówiąc, efekt z oglądania
dowodów będzie mizerniutki.
Jean Pierre Fermat miał pomysł (jeden z wielu !), że wszystkie liczby o
postaci
22k +1 są liczbami pierwszymi (pamiętasz, dla liczb p naprawdę
pierwszych o tej postaci, Gauss udowodnił możliwość ,,Euklidesowej'' konstrukcji
regularnego p-kąta). Dla k=0,1,2,3 i 4 wszystko jest OK, ale już Euler (ca. 1735)
zauważył, że
225 +1 dzieli się przez 641. Wykazanie tego, korzystając z
kongruencji, jest szybkie, łatwe i przyjemne. W języku ,,przystawania'' mamy
wykazać, że:
W tym celu musimy w liczbie 641 doszukać się podobnej struktury, jak
w
232 + 1.
Dość oczywisty pomysł (ważne są potęgi dwójki!), to:
A więc
Wykorzystajmy teraz własność (6) - k=4:
W naszej
225 +1 mamy jednak tylko potęgę (32-gą) dwójki, a nie
uświadczysz w niej potęgi piątki. Musimy znaleźć jakąś kongruencją (modulo 641)
która zachodzi między potęgami dwójki i piątki. Każdy widzi, że 54 to 625,
które odległe jest od 641 o 16 = 24. Jesteśmy w domu:
I już możemy wykazać, że nie jest możliwa euklidesowa konstrukcja
225 +1-kąta foremnego:
Sympatyczna liczba Mersenne'a
283 - 1 (postulowana przez swojego patrona jako
kandydatka na liczbę pierwszą) dzieli się przez 167 (to też pokazał Euler).
Tutaj dwójka występuję w potędze przeszło dwa i pół raza większej niż w
poprzednim przykładzie. To nic, trzeba pobawić się w podnoszenie do kwadratu i
szukać partnerów kongruentnych (modulo 167) dla kolejnych potęg:
Teraz tylko pozostało inteligentne rozpisanie 83-ej potęgi dwójki.
83 = 16 + 67. A
67 nie jest dalekie od 64:
Jesteśmy w domu:
Quod erat demonstrandum.
Podoba się? No to, do roboty. Kilka nie za trudnych i sympatycznych problemików:
- Udowodnij:
- Czy 536 -1 dzieli się przez 13? A
1049 + 53 przez 7?
- Jaką resztę otrzymasz z dzielenia sumy:
przez 12? (Na wszelki przypadek, pozwalam sobie zauważyć, że 12 to 4!)
Nie podaję rozwiązań. Ale zawsze służę (p)odpowiedzią, jeżeli ktoś ładnie
poprosi.
Miłego przystawania do teorii liczb!




Next: "Nie samą matematyką ..."
Up: Carl Friedrich Gauss
Previous: Carl Friedrich Gauss
Andrzej Lenda
1999-06-15