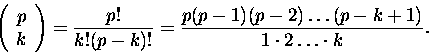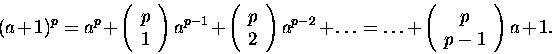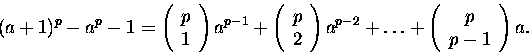Next: Pierwsze próbkowanie ...
Up: Kilka drobiazgów z historii
Previous: Paradoks petersburski
 Pierre Fermat (1601-1665) nazywany był słusznie ,,księciem amatorów'' - będąc z wykształcenia i zawodu prawnikiem (studiował
prawo na uniwersytecie w Tuluzie i Orleanie) może się poszczycić osiągnięciami
w rozwoju nauk matematycznych i fizycznych porównywalnymi z osiągnięciami najtęższych matematyków i fizyków
17. wieku. Jego oryginalne prace z geometrii analitycznej nie ustępowały pracom Kartezjusza (uważanego za ojca geometrii analitycznej), a
jego wkład do rozwoju rachunku prawdopodobieństwa jest nie mniejszy od
tego, jaki przedstawiają prace Pascala. Ale największą sławę
w świecie matematyków zawdzięcza Fermat swoim dwóm twierdzeniom,
nazywanym małym i dużym (lub ostatnim) twierdzeniem Fermata, a związanym z rozwijającą w 17. wieku teorią liczb.
Fermat zajmował się matematyką z pasją i talentem, ale nie
troszczył się zbytnio o rzetelne dokumentowanie swoich odkryć:
przypuszczeń, czy też twierdzeń. Prawdopodobnie, nie będąc
,,prawdziwym'' matematykiem nie czuł się zobowiązany do
detalicznego i rygorystycznego udodwadniania swoich śmiałych pomysłów, które
zresztą dla niego (tylko!) były oczywiste. Większość osiągnięć Fermata można znaleźć na ...marginesach jego
egzemplarza kompendium wiedzy matematycznej starożytnych Greków. Była to słynna Mathematica Diofantesa, opublikowana w latach
dwudziestych 17. wieku w wersji dwujęzycznej: grecki oryginał z łacińskim tłumaczeniem i komentarzami. (Mathematica pojawiła się
w nowożytnej Europie w drugiej połowie 16. wieku i została wówczas częściowo przełożona na łacinę przez Bombelliego.)
Właśnie na marginesach tej książki można znaleźć większość ,,notatek'' Fermata - po jego śmierci, syn Fermata, Samuel,
miał na szczęście świetny pomysł i spowodował reedycję
książki z wszystkimi glosami na marginesach. Ale marginesy były
niestety niezbyt szerokie - dlatego często wyjaśnienia, szkice dowod
ów są skrótowe i nie do końca jasne. Oprócz glos na
marginesach Mathematica Fermat pozostawił pewną liczbę listów
do przyjaciół-matematyków (Pascala, i Mersenne'a)
w których informuje ich o swoich
najnowszych
pomysłach, ale i w tym przypadku ogranicza się przeważnie do
podania treści twierdzeń, bez wnikania w szczegóły dowodów.
Należy pogratulować matematycznym przyjaciołom Fermata lojalności
- listy, które pisał do nich Fermat traktowane były z należytym pietyzmem i szacunkiem; powielane (kopiowane) krążyły w
ówczesnym ,,środowisku naukowym'' i spełniały - choć trochę
- rolę dzisiejszych publikacji.
Pierre Fermat (1601-1665) nazywany był słusznie ,,księciem amatorów'' - będąc z wykształcenia i zawodu prawnikiem (studiował
prawo na uniwersytecie w Tuluzie i Orleanie) może się poszczycić osiągnięciami
w rozwoju nauk matematycznych i fizycznych porównywalnymi z osiągnięciami najtęższych matematyków i fizyków
17. wieku. Jego oryginalne prace z geometrii analitycznej nie ustępowały pracom Kartezjusza (uważanego za ojca geometrii analitycznej), a
jego wkład do rozwoju rachunku prawdopodobieństwa jest nie mniejszy od
tego, jaki przedstawiają prace Pascala. Ale największą sławę
w świecie matematyków zawdzięcza Fermat swoim dwóm twierdzeniom,
nazywanym małym i dużym (lub ostatnim) twierdzeniem Fermata, a związanym z rozwijającą w 17. wieku teorią liczb.
Fermat zajmował się matematyką z pasją i talentem, ale nie
troszczył się zbytnio o rzetelne dokumentowanie swoich odkryć:
przypuszczeń, czy też twierdzeń. Prawdopodobnie, nie będąc
,,prawdziwym'' matematykiem nie czuł się zobowiązany do
detalicznego i rygorystycznego udodwadniania swoich śmiałych pomysłów, które
zresztą dla niego (tylko!) były oczywiste. Większość osiągnięć Fermata można znaleźć na ...marginesach jego
egzemplarza kompendium wiedzy matematycznej starożytnych Greków. Była to słynna Mathematica Diofantesa, opublikowana w latach
dwudziestych 17. wieku w wersji dwujęzycznej: grecki oryginał z łacińskim tłumaczeniem i komentarzami. (Mathematica pojawiła się
w nowożytnej Europie w drugiej połowie 16. wieku i została wówczas częściowo przełożona na łacinę przez Bombelliego.)
Właśnie na marginesach tej książki można znaleźć większość ,,notatek'' Fermata - po jego śmierci, syn Fermata, Samuel,
miał na szczęście świetny pomysł i spowodował reedycję
książki z wszystkimi glosami na marginesach. Ale marginesy były
niestety niezbyt szerokie - dlatego często wyjaśnienia, szkice dowod
ów są skrótowe i nie do końca jasne. Oprócz glos na
marginesach Mathematica Fermat pozostawił pewną liczbę listów
do przyjaciół-matematyków (Pascala, i Mersenne'a)
w których informuje ich o swoich
najnowszych
pomysłach, ale i w tym przypadku ogranicza się przeważnie do
podania treści twierdzeń, bez wnikania w szczegóły dowodów.
Należy pogratulować matematycznym przyjaciołom Fermata lojalności
- listy, które pisał do nich Fermat traktowane były z należytym pietyzmem i szacunkiem; powielane (kopiowane) krążyły w
ówczesnym ,,środowisku naukowym'' i spełniały - choć trochę
- rolę dzisiejszych publikacji.
Małe twierdzenie Fermata odnosi się do problemu podzielności liczb.
Problem ten jest ściśle związany z modnymi wówczas
poszukiwaniami liczb doskonałych (liczba doskonała to liczba, która
jest równa liczbie swoich podzielników - oczywiście pod warunkiem,
że odrzucimy samą liczbę jako ,,własny'' podzielnik. Na przykład: 6=1+2+3 lub
28=1+2+4+7+14.), poszukiwaniami które rozpoczęli
jeszcze matematycy w starożytnej Grecji.
Twierdzenie to ma postać:
Jeżeli p jest liczbą pierwszą, natomiast a - dowolną liczbą całkowita NIEPODZIELNĄ przez p, to wyrażenie
jest podzielne przez p.
Ogłoszone (podane bez dowodu w liście do przyjaciela) w 1640 roku
twierdzenie zostało ,,oficjalnie'' udowodnione przez Eulera, prawie sto
lat później, chociaż w rękopisach dzieł Leibniza można
znaleźć podobny (choć nie opublikowany) dowód, który Leibniz
musiał przeprowadzić nie później niż w 1683r.). Dowód
Cauchy'ego oparty o metodę indukcji matematycznej, połączoną
z dwumianem Newtona, prościej jest przeprowadzić dla twierdzenia sformułowanego w postaci nieco ,,prostszej'' :
udowadniamy podzielność przez p wyrażenia ap - a .
(Wytłumacz sobie równoważność obu sformułowań!).
Po pierwsze: jeżeli p jest liczbą pierwszą
to współczynniki dwumianowe
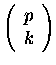 są podzielne przez p dla wszystkich
są podzielne przez p dla wszystkich
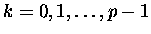 .
Wynika to z ich definicji:
.
Wynika to z ich definicji:
Licznik prawej strony jest ewidentnie podzielny przez p, a ponieważ w
mianowniku występują czynniki z pewnością od p mniejsze to cała prawa strona - a więc i prawa - jest przez p podzielna.
Po drugie: metoda indukcji pozwala łatwo wówczas wykazać prawdziwość twierdzenia.
Dla p=1 ap - a jest równe zeru, a zero jest
podzielne przez wszystko. Jeżeli ten sprawdzian Cię nie zadawala to
dla p=2 mamy
ap-a = a2 - a = a(a-1). Taki iloczyn dwóch
kolejnych liczb całkowitych musi być parzysty.
Kolejny krok dowodu indukcyjnego to przyjęcie: ap-a (a - dowolne, całkowite) podzielne przez p i wykazanie w oparciu o ten postulat tezy
dla a+1. Wzór Newtona daje
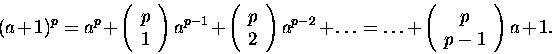 |
(1.5) |
Po przeniesieniu pierwszego i ostatniego wyrazu z prawej strony na lewą
dostajemy
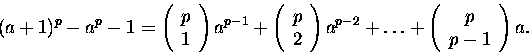 |
(1.6) |
Zgodnie z przedstawioną przed chwilą argumentacją, prawa strona
jest podzielna przez p, a więc p dzieli też wyrażenie
(a+1)p-ap-1. Ponieważ, z założenia dzieli też ap-a, to
dzielić będzie sumę obu
Proste. Tylko nie zapominaj, że metodę indukcji matematycznej trzysta
lat temu potrafiło skutecznie zastosować (dosłownie) kilku matematyków.
O ile ,,małe'' twierdzenie Fermata stosunkowo szybko przestało być
tajemnicą to ,,wielkie twierdzenie'' Fermata pogrążyło w otchłani frustracji świat matematyczny na trzy i pół wieku! Glosa na
marginesie powiększa jeszcze tę frustrację: Fermat pisze
explicite, że zna dowód ale ...nie zamieszcza go z braku miejsca!
Słynne twierdzenie jest zarazem ogromnie proste. Wszyscy znamy tzw.
liczby pitagorejskie - triady liczb całkowitych x,y i z spełniające równanie Pitagorasa:
x2+y2=z2.
Najbardziej chyba popularną trójcą jest 3,4,5 ale jest ich nieskończenie
wiele. Otóż ,,wielkie twierdzenie'' mówi, że
analogiczne równanie dla n>2
xn+yn=zn
nie ma rozwiązań ! (oczywiście w klasie liczb całkowitych).
Obecnie uważa się, że Fermat pisząc o swoim dowodzie miał
prawdopodobnie na myśli dowód (?) dla konkretnych wartości n, np.
n=3 lub n=4, ale najprawdopodobniej był bardzo (?) daleko od dowodu
ogólnego. O ten ostatni rozegrała się 350-letnia batalia. Wielokrotnie
pojawiali się zwycięzcy - ale ich dowody zawsze okazywały się
niekompletne. W latach siedemdziesiątych (20. wieku!) do pracy zaprzęgnięto
komputery, które (biedne) sumiennie przetestowały
prawdziwość fermatowskiego twierdzenia dla n dobrze ponad 100 000! Dowód
pojawił się w ostatnich latach. W lecie 1993, Andrew Wiles z
Uniwersytetu Princeton, przedstawił serię trzech wykładów,
200-stronicową dysertację i ...po prawie dwuletnich deliberacjach
świat matematyków wydał westchnienie ulgi. Dokonało się. Ale myślę, że gdzieś tam jeszcze długo (zawsze ?) pozostanie cień
podejrzenia: czy rzeczywiście Fermat nie miał lepszego pomysłu na
udowodnienie wielkiego twierdzenia te drobne 350 lat wcześniej?




Next: Pierwsze próbkowanie ...
Up: Kilka drobiazgów z historii
Previous: Paradoks petersburski
Andrzej Lenda
1999-03-08
 Pierre Fermat (1601-1665) nazywany był słusznie ,,księciem amatorów'' - będąc z wykształcenia i zawodu prawnikiem (studiował
prawo na uniwersytecie w Tuluzie i Orleanie) może się poszczycić osiągnięciami
w rozwoju nauk matematycznych i fizycznych porównywalnymi z osiągnięciami najtęższych matematyków i fizyków
17. wieku. Jego oryginalne prace z geometrii analitycznej nie ustępowały pracom Kartezjusza (uważanego za ojca geometrii analitycznej), a
jego wkład do rozwoju rachunku prawdopodobieństwa jest nie mniejszy od
tego, jaki przedstawiają prace Pascala. Ale największą sławę
w świecie matematyków zawdzięcza Fermat swoim dwóm twierdzeniom,
nazywanym małym i dużym (lub ostatnim) twierdzeniem Fermata, a związanym z rozwijającą w 17. wieku teorią liczb.
Fermat zajmował się matematyką z pasją i talentem, ale nie
troszczył się zbytnio o rzetelne dokumentowanie swoich odkryć:
przypuszczeń, czy też twierdzeń. Prawdopodobnie, nie będąc
,,prawdziwym'' matematykiem nie czuł się zobowiązany do
detalicznego i rygorystycznego udodwadniania swoich śmiałych pomysłów, które
zresztą dla niego (tylko!) były oczywiste. Większość osiągnięć Fermata można znaleźć na ...marginesach jego
egzemplarza kompendium wiedzy matematycznej starożytnych Greków. Była to słynna Mathematica Diofantesa, opublikowana w latach
dwudziestych 17. wieku w wersji dwujęzycznej: grecki oryginał z łacińskim tłumaczeniem i komentarzami. (Mathematica pojawiła się
w nowożytnej Europie w drugiej połowie 16. wieku i została wówczas częściowo przełożona na łacinę przez Bombelliego.)
Właśnie na marginesach tej książki można znaleźć większość ,,notatek'' Fermata - po jego śmierci, syn Fermata, Samuel,
miał na szczęście świetny pomysł i spowodował reedycję
książki z wszystkimi glosami na marginesach. Ale marginesy były
niestety niezbyt szerokie - dlatego często wyjaśnienia, szkice dowod
ów są skrótowe i nie do końca jasne. Oprócz glos na
marginesach Mathematica Fermat pozostawił pewną liczbę listów
do przyjaciół-matematyków (Pascala, i Mersenne'a)
w których informuje ich o swoich
najnowszych
pomysłach, ale i w tym przypadku ogranicza się przeważnie do
podania treści twierdzeń, bez wnikania w szczegóły dowodów.
Należy pogratulować matematycznym przyjaciołom Fermata lojalności
- listy, które pisał do nich Fermat traktowane były z należytym pietyzmem i szacunkiem; powielane (kopiowane) krążyły w
ówczesnym ,,środowisku naukowym'' i spełniały - choć trochę
- rolę dzisiejszych publikacji.
Pierre Fermat (1601-1665) nazywany był słusznie ,,księciem amatorów'' - będąc z wykształcenia i zawodu prawnikiem (studiował
prawo na uniwersytecie w Tuluzie i Orleanie) może się poszczycić osiągnięciami
w rozwoju nauk matematycznych i fizycznych porównywalnymi z osiągnięciami najtęższych matematyków i fizyków
17. wieku. Jego oryginalne prace z geometrii analitycznej nie ustępowały pracom Kartezjusza (uważanego za ojca geometrii analitycznej), a
jego wkład do rozwoju rachunku prawdopodobieństwa jest nie mniejszy od
tego, jaki przedstawiają prace Pascala. Ale największą sławę
w świecie matematyków zawdzięcza Fermat swoim dwóm twierdzeniom,
nazywanym małym i dużym (lub ostatnim) twierdzeniem Fermata, a związanym z rozwijającą w 17. wieku teorią liczb.
Fermat zajmował się matematyką z pasją i talentem, ale nie
troszczył się zbytnio o rzetelne dokumentowanie swoich odkryć:
przypuszczeń, czy też twierdzeń. Prawdopodobnie, nie będąc
,,prawdziwym'' matematykiem nie czuł się zobowiązany do
detalicznego i rygorystycznego udodwadniania swoich śmiałych pomysłów, które
zresztą dla niego (tylko!) były oczywiste. Większość osiągnięć Fermata można znaleźć na ...marginesach jego
egzemplarza kompendium wiedzy matematycznej starożytnych Greków. Była to słynna Mathematica Diofantesa, opublikowana w latach
dwudziestych 17. wieku w wersji dwujęzycznej: grecki oryginał z łacińskim tłumaczeniem i komentarzami. (Mathematica pojawiła się
w nowożytnej Europie w drugiej połowie 16. wieku i została wówczas częściowo przełożona na łacinę przez Bombelliego.)
Właśnie na marginesach tej książki można znaleźć większość ,,notatek'' Fermata - po jego śmierci, syn Fermata, Samuel,
miał na szczęście świetny pomysł i spowodował reedycję
książki z wszystkimi glosami na marginesach. Ale marginesy były
niestety niezbyt szerokie - dlatego często wyjaśnienia, szkice dowod
ów są skrótowe i nie do końca jasne. Oprócz glos na
marginesach Mathematica Fermat pozostawił pewną liczbę listów
do przyjaciół-matematyków (Pascala, i Mersenne'a)
w których informuje ich o swoich
najnowszych
pomysłach, ale i w tym przypadku ogranicza się przeważnie do
podania treści twierdzeń, bez wnikania w szczegóły dowodów.
Należy pogratulować matematycznym przyjaciołom Fermata lojalności
- listy, które pisał do nich Fermat traktowane były z należytym pietyzmem i szacunkiem; powielane (kopiowane) krążyły w
ówczesnym ,,środowisku naukowym'' i spełniały - choć trochę
- rolę dzisiejszych publikacji.
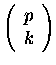 są podzielne przez p dla wszystkich
są podzielne przez p dla wszystkich
![]() .
Wynika to z ich definicji:
.
Wynika to z ich definicji: