Różniczkowanie funkcji f(x)
Do różniczkowania funkcji służy komenda diff(f,x), dzięki której funkcja (wcześniej zdefiniowana jako f z wprowadzonymi zmiennymi oraz parametrami symbolicznymi), będzie różniczkowana względem zmiennej x. Można również posłużyć się komendą diff(f). Funkcja będzie domyślnie różniczkowana po x-ach. Chcąc zróżniczkować funkcję f(x,a) = sin(ax) najpierw musimy wprowadzić x oraz a, a następnie odpowiednio zapisać f(x). W głównym oknie matlaba piszemy:
syms a x %wprowadzamy symboliczne a oraz x
f = sin(a*x) %zapisujemy postać funkcji f(x)
g = diff(f) %domyślnie różniczkujemy po x-ach
W odpowiedzi otrzymujemy funkcję g(x): g = cos(a*x)*a
h = diff(f,a) %różniczkuje funkcje f wzgledem a
W odpowiedzi otrzymujemy funkcję h(a): h = cos(a*x)*x
Do liczenia pochodnych wyższych rzędów służy komenda diff(f,x,2) gdzie f - to różniczkowana funkcja, x - oznacza po jakiej zmiennej funkcja będzie różniczkowana, a na końcu wpisujemy którą pochodną chcemy policzyć (w tym przypadku jest to druga pochodna, ale można wpisać dowolną). Można w tej komendzie tak jak poprzednio pominąć x, wtedy domyślnie policzona zostanie druga pochodna funkcji f względem x.
Różniczkowanie elementów macierzy A
Różniczkowanie można równie dobrze wykonywać na elemantach macierzy A diff(A)
syms a x %wprowadzamy symboliczne a oraz x
A = [cos(a*x),sin(a*x);-sin(a*x),cos(a*x)] %zapisujemy macierz
diff(A) %różniczkujemy każdy element macierzy
W odpowiedzi dostajemy
A =
[ -sin(a*x)*a, cos(a*x)*a]
[ -cos(a*x)*a, -sin(a*x)*a]
Tak jak przy funkcjach, można różniczkować względem dowolnej zmiennej oraz można liczyć różniczki wyższych rzędów.
Jakobian
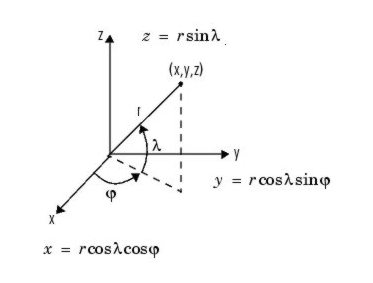
Jeśli układ współrzędnych sferycznych zdefiniowany jest jak na rysunku:

to jakobian
wyraża się wzorem:
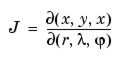
W Matlabie jakobian oblicza się komendą J = jacobian([x; y; z], [r l f]).
l = sym('lambda'), r = sym('ro'), f = sym('phi') % wprowadzamy zmienne współrzędnych sferycznych l czyli lambda, r czyli ro oraz f czyli phi
x = r*cos(l)*cos(f); y = r*cos(l)*sin(f); z = r*sin(l); % zapisujemy związki między współrzędnymi przestrzennymi a współrzędnymi sferycznymi
J = jacobian([x; y; z], [r l f]) % liczymy jakobian
W odpowiedzi dostajemy
J =
[ cos(lambda)*cos(phi), -ro*sin(lambda)*cos(phi), -ro*cos(lambda)*sin(phi)]
[ cos(lambda)*sin(phi), -ro*sin(lambda)*sin(phi), ro*cos(lambda)*cos(phi)]
[ sin(lambda), ro*cos(lambda), 0]
Całkowanie funkcji f(x)
Przy liczeniu całek obowiązują te same reguły co przy liczeniu różniczek. Całki można liczyć nieokreślone: int(f,x) (wystarczy napisać inf(f) wtedy funkcja zostanie domyślnie scałkowana po dx). Lub określone w przedziale (a.b): int(f,x,a,b).
Zachęcam do przećwiczenia takich samych wariantów z tą komendą jak z komendą diff(x).
Granice funkcji
Gdy wprowadzimy symboliczne wyrażenie S(n), to jego granicę przy n dążącym do jakiejś wartości a możemy wyliczyć przy pomocy komendy
limit(S,n,a) %liczymy granicę z wyrażenia S przy n dążącym do a.
Pochodną funkcji można wyliczyć z definicji, licząc następującą granicę:
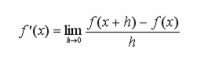
Za pomocą komendy limit(S,n,a) możemy policzyć pochodną funkcji.Gdy chcemy policzyć pochodną funkcji f(x) = sin(x) w głównym oknie Matlaba wpisujemy:
syms x h %wprowadzamy symbolicznie x oraz h
S = (sin(x+h) - sin(x))/h %zapisujemy wyrażenie na S
g = limit(S,h,0 ) %wyliczamy granice z S przy h dążącym do 0
To samo można zrobić w następujący sposób:
syms x h
limit((sin(x+h) - sin(x))/h,h,0)
Domyślnie liczona jest granica dążąca do 0. Mozna liczyć również granice do nieskończoności wpisując inf za n-em w nawiasie limit( (1 + x/n)^n,n,inf ), lub -inf gdy liczymy granicę w minus nieskończoności. Są funkcje takie jak np.: f(x) = 1/x nieokreślone w zerze. Liczymy wtedy granicę przy x zmierzającym do zera z prawej 'right' lub lewej 'left' strony. 'right' lub 'left' wpisujemy na końcu nawiasu limit(1/x,x,0,'left').
Sumowanie szeregów
Komendą symsum(S,n,a,b) dokonujemy sumowania szeregu S po n-ach od a do b
syms n
S = 1/n^2 %zapisujemy wyrażenie S(n)
symsum(S,n,1,inf) %sumujemy od 1 do nieskończoności
ans = 1/6*pi^2 %odpowiedź
Szereg Taylora jednej zmiennej
Komendą taylor(f,n,a) rozwijamy funkcję f w szereg Taylora do n-tego rzędu, względem a, według wzoru
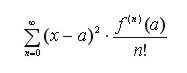
syms x
f = exp(x^2) %zapisujemy funkcję f(x)
t = taylor(f,4,1) %rozwijamy w szereg Taylora względem jedynki i do czwartego rzędu
t = exp(1)+2*exp(1)*(x-1)+3*exp(1)*(x-1)^2+10/3*exp(1)*(x-1)^3 %odpowiedź
Do wyrażenia t proponuję zastosować komendę pretty(t).