3. Derivation of Eq.(3)
Derivation of Eq. 3 utilizes the approach and nomenclature from kinematic theory of X-ray diffraction on crystals. It is divided into three steps (a)-(c).
a) formfactor of a single trapezium
For the flat 2D aperture located at x-y plane, the general formula (2) is reduced to:
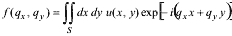
For our aperture u(x, y) = 1 inside the area of trapezium and u(x, y) = 0 outside. Thus:
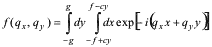
A straightforward calculations of this integral leads to
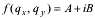
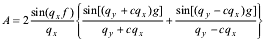
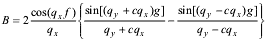
Formfactor of a single trapezium contains both real (A) and imaginary (B) components, because trapezium does not contain the inversion point.
b) formfactor of the unit cell
Primitive unit cell (Fig. 5B) contains two trapeziums. Formfactor of the central trapezium was calculated above. For the second
trapezium (composed from four sections located in unit cell corners) the slope coefficient c is replaced by -c, hence its formfactor is given by A - iB.
The choice of h, k indices used in this work is based on the unit vectors
a0 and
b0. (Fig. 5A). Within this
base the dimensionless positions u, v and the formfactors for trapeziums contained in a unit cell are given by:
central trapezium : u = 0 v = 0 f = A + iB
inverted trapezium: u = 1 v = 0 f = A - iB
Formfactor of the primitive unit cell is calculated in analogy to the well-known formula in crystallography, with trapeziums corresponding to atoms.
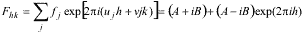
For main spots (integer h and k) Fhk = 4A, for superlattice spots (half-integer h and k) Fhk = 4B. Both formfactors are real functions because
the considered unit cell has a center of inversion.
c) integrated spot intensity for an infinite lattice
Spot intensity is proportional to the square of Fhk calculated for values of scattering vector
qx = (2p/a0)h, qy = (2p/b0)k,
representing points of the reciprocal lattice. These intensities related to the intensity of the central spot I00 are given by
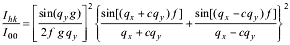 , for main spots, and , for main spots, and
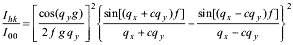 , for superstructure spots. , for superstructure spots.
|
d) numerical parameters for model calculations
Geometry of the fabric is defined by thread-thread distance d = 169 mm and thread diameter 2r = 51 mm (Fig. 1).
The parameters of the trapezium model as a function of the inclination angle ω are given by:
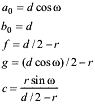
The formulae given above were derived under assumption that fabric threads are circular cylinders.
The photograph (Fig. 1) shows that they are flattened at the thread crossing.
The effect of flattening may qualitatively account for the shift of maximum of I(ω) calculated curve in Fig. 2 leftwards with respect to experiment.