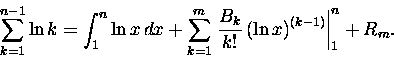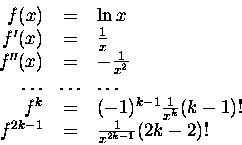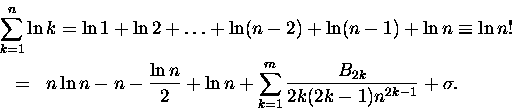Next: Literatura ...
Up: Liczby przeróżne
Previous: Liczby Bernoulliego
Jeżeli życie nie jest znowu takie różowe to trzeba przyglądnąć się reszcie RR2q,
albo - będzie prościej pisać - reszcie Rm. Jej nieco zmodyfikowana postać to:
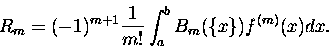 |
(1) |
(Całkujemy po pewnym - skończonym, albo i nie - przedziale x-a; 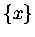 to część
ułamkowa z x-a.)
to część
ułamkowa z x-a.)
Przy takim zapisie wzór sumacyjny Eulera-Maclaurina wygląda
Intuicyjnie czujemy, że różnica Rm nie powinna być większa niż pierwszy wyraz, z
którego zrezygnowaliśmy w sumie, innymi słowy możemy zawsze oszacować różnicę
jako
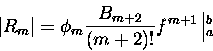 |
(3) |
gdzie 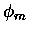 to pewna liczba z przedziału (0,1). (Skaczemy ze wskaźnikiem liczb Bernoulliego o dwa,
bo - jak pamiętamy - praktycznie tylko parzyste są różne od zera; z tego wniosek, że w praktyce
wskaźnik m też zawsze powinien być parzysty.)
to pewna liczba z przedziału (0,1). (Skaczemy ze wskaźnikiem liczb Bernoulliego o dwa,
bo - jak pamiętamy - praktycznie tylko parzyste są różne od zera; z tego wniosek, że w praktyce
wskaźnik m też zawsze powinien być parzysty.)
Chciałoby się, aby wzór 1 zachowywał jakoś ,,grzecznie''. Na przykład przy m
rosnącym aby Rm spadało (pardon, dążyło) do zera. Nic z tego - wcale tak nie jest. Skąd
inąd reszta Rm potrafi dążyć do pewnej granicy, ale tak jest jeżeli rozpatrujemy w naszej
sumie 2 baardzo dużo - nieskończenie wiele wyrazów - przedział (a,b) (całki), albo (a,b-1) sumy
staje się praktycznie nieskończony. Brzmi to skomplikowanie - dlatego spróbujmy prześledzić pewien
pożyteczny przykład, który powinien nam nieco rozjaśnić w głowie.
Przypuśćmy, że chcemy policzyć sumę nieskończoną:
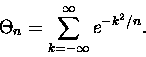 |
(4) |
Twór występujący pod znakiem sumy to coś, co możnaby nazwać
"zdyskretyzowanym
rozkładem Gaussa" (w dodatku pozbawionym stałej normalizacyjnej). Jak pamiętamy ,,zwykły''
rozkład Gaussa (o wartości oczekiwanej = 0) to
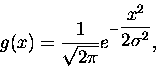 |
(5) |
i każdy (!) wie, że
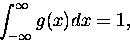 |
(6) |
a także, że wkład do tej całki pochodzi głównie od pierwszych dwóch (czterech, no
sześciu) przedziałów o szerokości 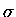 ,
usytuowanych symetrycznie wokół zera. W
naszej sumie
,
usytuowanych symetrycznie wokół zera. W
naszej sumie 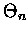 rolę odchylenia standardowego odgrywa
rolę odchylenia standardowego odgrywa
Czyli odchylenie standardowe - naturalna jednostka zmiennej x - jest proporcjonalne do 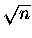 .
No tak,
w takim razie suma 4 powinna być proporcjonalna do
.
No tak,
w takim razie suma 4 powinna być proporcjonalna do
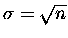 (bo składa się na te sumę
parę ,,prostokącików'' których podstawa to właśnie
(bo składa się na te sumę
parę ,,prostokącików'' których podstawa to właśnie 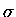 ). Zresztą z 5 i 6
każdy widzi, że
). Zresztą z 5 i 6
każdy widzi, że
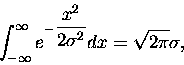 |
(7) |
albo
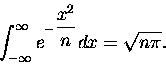 |
(8) |
Nasza  będzie więc równa - wzór 2 -
będzie więc równa - wzór 2 -
Występujące powyżej wartości pochodnych
są wszystkie równe zeru, bo nasza
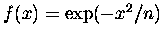 ,
a każda pochodna takiej funkcji zawiera ją w
sobie w formie czynnika, który to czynnik elegancko zeruje się w dodatniej i ujemnej
nieskończoności. Tak więc nasza
,
a każda pochodna takiej funkcji zawiera ją w
sobie w formie czynnika, który to czynnik elegancko zeruje się w dodatniej i ujemnej
nieskończoności. Tak więc nasza 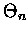 wygląda prościutko
wygląda prościutko
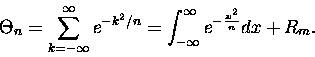 |
(10) |
I teraz każdy widzi, że reszta Rm jest najważniejsza. W zależności od wartości n (a
więc odchylenia standardowego) sumy muszą być nieco różne. Małe n - dyskretny
rozkład Gaussa jest stosunkowo ,,ostry''; duże n - bardziej rozprostowany. Jeżeli tak, to dla
małych n ,,poprawka'' do całki (dla sumy  )
będzie większa, a dla większych -
mniejsza. Możesz to oglądnąć na dwóch rysunkach pierwszy
)
będzie większa, a dla większych -
mniejsza. Możesz to oglądnąć na dwóch rysunkach pierwszy
, ,
to ,,dyskretny'' i ,,zwykły''
Gauss dla n=2, a drugi
,
to ,,dyskretny'' i ,,zwykły''
Gauss dla n=2, a drugi
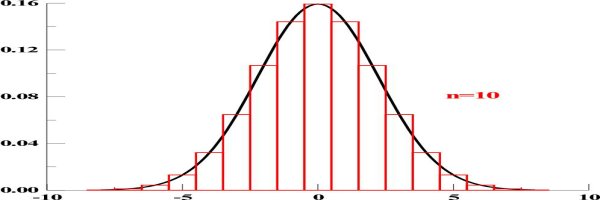 ,
- dla n=10.
,
- dla n=10.
Widać, że im większe n tym zgodność obu typów
jest lepsza, a więc rola reszty Rm - mniejsza.
Sęk jednak w tym, że dla określonego n reszta zawsze będzie różna (większa - to dośc łatwo można wykazać) od zera, a
jej obliczenie - no, nie jest za proste. Matematycy konkretni robią to - o zgrozo - nieco bałamutnie, ale -
na szczęście - podają w końcu dobry wzór, a także sposób w jaki można się go
dorobić. Ten wzór to
a sposób ten to transformata Fourriera. Zauważ, że resztę nazwaliśmy R ze wskaźnikiem
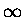 - bo nikt nam nie broni przejść z m do nieskończoności, a dodatkowo
zaakcentowaliśmy jej zależność od odchylenia standardowego naszego dyskretnego Gaussa, to
znaczy od n.
- bo nikt nam nie broni przejść z m do nieskończoności, a dodatkowo
zaakcentowaliśmy jej zależność od odchylenia standardowego naszego dyskretnego Gaussa, to
znaczy od n.
Ta reszta jest naprawdę malutka. Dla n=2 wartość sumy 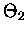 to z grubsza 2,506628288, a
to z grubsza 2,506628288, a
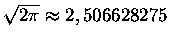 - różnica występuje na siódmym miejscu po przecinku. Dla
- różnica występuje na siódmym miejscu po przecinku. Dla
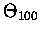 różnica wystepuje dopiero na 428. miejscu po przeci
różnica wystepuje dopiero na 428. miejscu po przeci
nku (proszę, sa tacy, ktorzy potrafia to policzyć!).
Jeżeli nie masz jeszcze dosyć, to zapraszam do oglądnięcia sposobu, w jaki metoda Eulera-
Maclaurina pozwala się dorobić znanego wzoru Stirlinga, stanowiącego przybliżenie silni (n!),
bardzo przydatnego dla dużych wartości n. To znaczy wzór potrafimy bez kłopotu
wyprowadzić tak jak uczynił to 270 lat temu pan De Moivre. Miał on wówczas postać
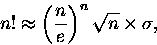 |
(11) |
gdzie - tym razem - 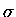 oznacza pewna stałą. De Moivre nie potrafił tej stałej wyliczyć, i
dopiero jego dobry kolega matematyk, doszedł, że jest ona równa
oznacza pewna stałą. De Moivre nie potrafił tej stałej wyliczyć, i
dopiero jego dobry kolega matematyk, doszedł, że jest ona równa
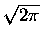 ,
co De Moivre
skrupulatnie zaznaczył w kolejnym wydaniu (A.D. 1738) swojej - zresztą poświęconej
głównie statystyce - Doctrine of chances, pisząc: I desisted in proceeding farther till my
worthy friend Mr. James Stirling, who had applied after me to that inquiry, discovered that
,
co De Moivre
skrupulatnie zaznaczył w kolejnym wydaniu (A.D. 1738) swojej - zresztą poświęconej
głównie statystyce - Doctrine of chances, pisząc: I desisted in proceeding farther till my
worthy friend Mr. James Stirling, who had applied after me to that inquiry, discovered that
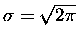 .'' Czyż nie ładnie? Przez psikus historii wzór nazywa się wzorem Strirlinga, chociaż
- jak zobaczymy - de Moivre też ma tu zasadniczy udział.
.'' Czyż nie ładnie? Przez psikus historii wzór nazywa się wzorem Strirlinga, chociaż
- jak zobaczymy - de Moivre też ma tu zasadniczy udział.
Zobaczmyż więc. Jeżeli nasza funkcja f(x)jest poczciwym logarytmem:
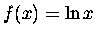 to w zgodzie z
wzorem uniwersalnym 2
to w zgodzie z
wzorem uniwersalnym 2
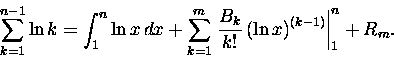 |
(12) |
Pochodne
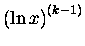 liczą się łatwiutko:
liczą się łatwiutko:
W sumie pochodnych jak zwykle wyodrębniamy pierwszy wyraz (ten z
B1 = -1/2).
Całkę z
logarytmu każdy wie jak policzyć:
Uff! W drugiej linijce całka i wyraz z B1, w trzeciej sumy pochodnych liczonych dla x=n i x=1, no
i reszta. Zapisałem ją Rm(n), aby podkreślić, że zależy ona jednak zarówno od n jak i
m. W gruncie rzeczy jednak, dla sensownych (nie drastycznie małych) m, a zwłaszcza n ta reszta
jest ,,prawie'' stała. Dla
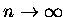 nasza reszta bardzo słabo zależy od m, a zupełnie
nie zależy od n - oznaczmy ją jako
nasza reszta bardzo słabo zależy od m, a zupełnie
nie zależy od n - oznaczmy ją jako
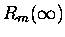 .
Od n nie zależy z całą
pewnością wartość drugiej z sum w powyższym wzorze. Wprowadźmy oznaczenie:
.
Od n nie zależy z całą
pewnością wartość drugiej z sum w powyższym wzorze. Wprowadźmy oznaczenie:
I jeszcze dodajmy do obu stron równania 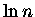 .
Voila!
.
Voila!
Pozostaje obłożenie obu stron powyższego wzoru funkcją wykładniczą:
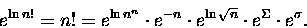 |
(14) |
Duże 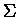 w wykładniku to suma zależna od n we wzorze 14. Pierwsze jej wyrazy to
w wykładniku to suma zależna od n we wzorze 14. Pierwsze jej wyrazy to
Już dla n=10
a
Bez większych więc ceregieli połóżmy
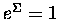 .
A w takim razie rzeczywiście
.
A w takim razie rzeczywiście
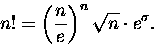 |
(15) |
Wzór będzie OK jeżeli przyjąć, że
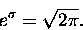 |
(16) |
Ba, ale jak to wykombinować? Jeden ze sposobów, sprytny a w dodatku korzystający z wyniku
sumowania
,,dyskretnego'' Gaussa (vide supra) znajdziesz w Matematyce Konkretnej. Nie wiem, niestety, czy tak
właśnie kombinował pan S. Pewnie i nie. Ale sposób jest sprytny - warto go oglądnąć. A
jeżeli Cię to wciągnie to ,,obok'' znajdziesz sposób na przybliżone (asymptotyczne) określenie
n-tej liczby harmonicznej Hn:
i zrozumiesz jak wyliczono dzielnemu robaczkowi czas jego wędrówki po gumowej taśmie.




Next: Literatura ...
Up: Liczby przeróżne
Previous: Liczby Bernoulliego
Andrzej Lenda
1999-08-18
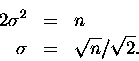
![]() będzie więc równa - wzór 2 -
będzie więc równa - wzór 2 -
 ,
to ,,dyskretny'' i ,,zwykły''
Gauss dla n=2, a drugi
,
to ,,dyskretny'' i ,,zwykły''
Gauss dla n=2, a drugi
 ,
- dla n=10.
,
- dla n=10.
![]() to z grubsza 2,506628288, a
to z grubsza 2,506628288, a
![]() - różnica występuje na siódmym miejscu po przecinku. Dla
- różnica występuje na siódmym miejscu po przecinku. Dla
![]() różnica wystepuje dopiero na 428. miejscu po przeci
różnica wystepuje dopiero na 428. miejscu po przeci
![]() to w zgodzie z
wzorem uniwersalnym 2
to w zgodzie z
wzorem uniwersalnym 2