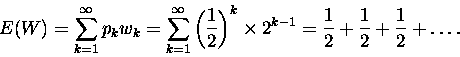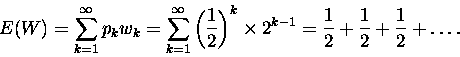Next: Pierre Fermat
Up: Rodzina Bernoullich
Previous: Rodzina Bernoullich
Gracz A rzuca monetą, do momentu aż wyrzuci orła.
Załóżmy, że następuje to w n-tym rzucie.
Gra się kończy, a gracz A dostaje od krupiera premię,
która wynosi 2n-1 rubli (jak Petersburg, to Petersburg!), a więc : 1, 2, 4, 8... Ile powinien
wpłacić
krupierowi gracz A, aby gra ,,była uczciwa'', to znaczy aby wartość oczekiwana wygranej była
równa
wpłaconej kwocie? Rozwiązanie
paradoksu nie jest łatwe. Prawdę mówiąc - nie doczekaliśmy się jeszcze w pełni
satysfakcjonującego
rozwiązania. Problem
sprowadza się do obliczenia wartości wygranej E(W) gracza A, a ta okazuje się ...
nieskończenie
wielka!
Rzeczywiście, oznaczając przez pk prawdopodobieństwo zakończenia gry w k-tym rzucie, a
przez wk
wygraną wówczas premię (2k-1)
mamy
Czyli gracz A - statystycznie - zawsze ma szanse wygrać,
niezależnie od tego jaki kapitał początkowy wpłaci do krupierowi!
Kłóci się ten wynik z naszym ,,zdrowym'' rozsądkiem, a także z ...doświadczalnymi
próbami wyznaczenia
E(W). Słynny markiz de Buffon (ten od określania wartości liczby 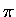 metodami losowymi)
przeprowadził
2048 prób. W 1061 orzeł wypadł za pierwszym razem, w 494 - za drugim, w 232 - za trzecim, w 137 -
- za
czwartym, w 56 - za piątym. Kolejne wyniki to:
29 gier z orłem w szóstym rzucie, 25 - w siódmym, 8 - w ósmym, 6 - w dziewiątym. Łatwo
policzyć, że suma
premii w tych 2048 grach wyniosłaby 10 057 rubli, z czego wynika, że E(W) miałaby wynosić
niecałe 5 rubli.
Petersburski paradoks był dyskutowany przez wielu słynnych matematyków i ...dalej pozostaje
paradoksem.
Dla pocieszenia - spróbuj policzyć E(W) dla premii wynoszącej q rubli, przy 0 < q <2.
Na przykład dla q=1,5 E(W) = 2.
metodami losowymi)
przeprowadził
2048 prób. W 1061 orzeł wypadł za pierwszym razem, w 494 - za drugim, w 232 - za trzecim, w 137 -
- za
czwartym, w 56 - za piątym. Kolejne wyniki to:
29 gier z orłem w szóstym rzucie, 25 - w siódmym, 8 - w ósmym, 6 - w dziewiątym. Łatwo
policzyć, że suma
premii w tych 2048 grach wyniosłaby 10 057 rubli, z czego wynika, że E(W) miałaby wynosić
niecałe 5 rubli.
Petersburski paradoks był dyskutowany przez wielu słynnych matematyków i ...dalej pozostaje
paradoksem.
Dla pocieszenia - spróbuj policzyć E(W) dla premii wynoszącej q rubli, przy 0 < q <2.
Na przykład dla q=1,5 E(W) = 2.




Next: Pierre Fermat
Up: Rodzina Bernoullich
Previous: Rodzina Bernoullich
Andrzej Lenda
1999-03-08