


Next: Magia i mistyka liczb;
Up: Kilka drobiazgów z historii
Previous: Pierre Fermat
W połowie 15. wieku problemem No.1 matematyki stało się
rozwiązanie
równanie trzeciego stopnia. Można powiedzieć, że czas był to
najwyższy!
Równanie drugiego stopnia umieli już rozwiązywać ...
rachmistrze
sumeryjscy, 2000 lat przed Chrystusem.
Przez niewytłumaczalny kaprys historii rozwoju
ludzkiego intelektu problem ,,o stopień wyższy'' czekał na
rozwiązanie
następne trzy i pół tysiąca lat.
Rozwiązanie równanie trzeciego stopnia wiąże się zazwyczaj z
nazwiskiem
Girolamo Cardano (1501-1576), chociaż wydaje się, że ten
niewątpliwie
wszechstronny uczony - prawdziwy ,,człowiek Renesansu'' wykorzystał
w
swoich dziełach Practica Mathematicae (1539) i Ars Magna
(1545)
wyniki uzyskane przez współczesnego mu (i z pewnością nie
ustępującego rangą) Nicolo Tartaglia (1500-1557) , który
zresztą
również
,,inspirował'' się wynikami działającego o pół wieku
wcześniej
Bolończyka
Scipione del Ferro (1465-1526).
Technika znalezienia pierwiastków równania
x3 + ax2 + bx + c = 0
polegała na sprowadzeniu równania -
poprzez
podstawienie
- do pozbawionego wyrazu z drugą potęgą równania:
y3 = py + q.
To właśnie Tartaglia pokazał, że ostatnie równanie ma
rozwiązanie
Jak nietrudno zauważyć, dla
(q/2)2 < (p/3)3 wielkość
występująca pod
kwadratowym pierwiastkiem staje się ujemna. I tak na przykład
,,historyczne
równanie'', opisywane przez Rafaela Bombelliego, ostatniego z wielkich
bolońskich matematyków 16. wieku
miałoby mieć - zgodnie ze wzorem Cardana-Tartaglii - rozwiązanie
![\begin{displaymath}
x = \sqrt[3]{2 + \sqrt{-121} } + \sqrt[3]{2 - \sqrt{-121} }.
\end{displaymath}](img32.gif) |
(1.8) |
Występujące pod kwadratowym pierwiastkiem -121 przeczyło
zdrowemu
(szesnastowiecznemu) rozsądkowi. Ale Bombelli wiedział, że
rozwiązaniem
równania 1.7
są ,,prawdziwe'' (rzeczywiste liczby): 4 oraz
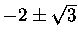 .
Rewolucyjny pomysł Bombelliego polegał na założeniu, że
występujące w
rozwiązaniu 1.8 pierwiastki trzeciego stopnie to
liczby zespolone,
będące sumą liczby ,,zwykłej'' (rzeczywistej) i ,,urojonej'' -
powstającej
z przemnożenia pewnej liczby rzeczywistej przez
.
Rewolucyjny pomysł Bombelliego polegał na założeniu, że
występujące w
rozwiązaniu 1.8 pierwiastki trzeciego stopnie to
liczby zespolone,
będące sumą liczby ,,zwykłej'' (rzeczywistej) i ,,urojonej'' -
powstającej
z przemnożenia pewnej liczby rzeczywistej przez 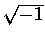 .
W dodatku oba pierwiastki trzeciego stopnia powinny się różnić
między sobą pojawiającym
się w sumie części rzeczywistej i urojonej znakiem, w sposób
identyczny
do tego w jaki różnią się wielkości występujące pod
znakiem
pierwiastka, to znaczy
.
W dodatku oba pierwiastki trzeciego stopnia powinny się różnić
między sobą pojawiającym
się w sumie części rzeczywistej i urojonej znakiem, w sposób
identyczny
do tego w jaki różnią się wielkości występujące pod
znakiem
pierwiastka, to znaczy
gdzie 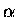 i
i 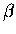 należałoby wyznaczyć. Przy takim
założeniu:
należałoby wyznaczyć. Przy takim
założeniu:
Ostatnie równość będzie spełniona, jeżeli
Powyższe równania mają - w klasie liczb całkowitych -
rozwiązania
dla
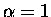 lub 2, oraz dla
lub 2, oraz dla 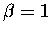 lub 11. Bliższa analiza
wykazuje,
że
jedyny akceptowalny wybór to
lub 11. Bliższa analiza
wykazuje,
że
jedyny akceptowalny wybór to
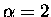 i
i 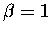 ,
a więc
rozwiązaniem 1.8 będzie
,
a więc
rozwiązaniem 1.8 będzie
W ten sposób właśnie pojawiły się ,,liczby zespolone'',
zawierające
w sobie
urojoną (a więc nieistniejącą) wielkość - kwadratowy
pierwiastek z
-1.
Przez przeszło dwieście lat pozostawały pełną abstrakcją
matematyczna -
abstrakcją, która odpowiednio manipulowana mogła jednak
doprowadzić
do
realnych wyników.
Dopiero na początku osiemnastego wieku powstała nowa koncepcja -
wykorzystania tych tworów matematycznych do opisu płaszczyzny. Tak
jak
zbiór liczb rzeczywistych można w sposób jedno-jednoznaczny
przedstawić
przy pomocy osi liczbowej x (każdy punkt osi odpowiada pewnej liczbie
rzeczywistej od 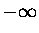 do
do 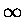 i odwrotnie), tak można
wprowadzić
jedno-jednoznaczne przyporządkowanie pomiędzy parami liczb i
punktami
płaszczyzny. Uporządkowaną parę liczb (a,b) traktować
możemy
jako
współrzędne końca wektora, którego początek pokrywa
się z
początkiem
układu współrzędnych. Osie tego układu to dwie
,,tradycyjne'' osie
liczbowe,
0x i 0y, z tym, że jednostką osi 0x jest 1, a osi 0y -
urojona
jednostka to
i odwrotnie), tak można
wprowadzić
jedno-jednoznaczne przyporządkowanie pomiędzy parami liczb i
punktami
płaszczyzny. Uporządkowaną parę liczb (a,b) traktować
możemy
jako
współrzędne końca wektora, którego początek pokrywa
się z
początkiem
układu współrzędnych. Osie tego układu to dwie
,,tradycyjne'' osie
liczbowe,
0x i 0y, z tym, że jednostką osi 0x jest 1, a osi 0y -
urojona
jednostka to
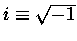 .
Te jednostki spełniają
jednocześnie
role
wersorów osi, w tym sensie że dowolny punkt na
płaszczyźnie zespolonej
(zwanej też płaszczyzną Arganda) możemy przedstawić jako
.
Te jednostki spełniają
jednocześnie
role
wersorów osi, w tym sensie że dowolny punkt na
płaszczyźnie zespolonej
(zwanej też płaszczyzną Arganda) możemy przedstawić jako
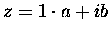 .
Współrzędna x-owa, (a) to część rzeczywista liczby zespolonej, natomiast
współrzędna
y-
owa -
b to jej część urojona. Analogicznie mówimy o
rzeczywistej
osi
0x
i osi urojonej 0y płaszczyzny 0xy.
W dalszym jednak ciągu przydatność liczb zespolonych była
mało
widoczna. Można ich było użyć
do
zgrabnego zapisu pewnych operacji na wektorach w przestrzeni
dwuwymiarowej na płaszczyźnie.
Dopiero w drugiej połowie 19. wieku zaczęła się objawiać
potęga
algebry
liczb zespolonych, a zwłaszcza teorii funkcji zmiennej zespolonej.
W
fizyce wielkości zespolone mają często znakomitą
interpretację
formalną -
np. zespolony współczynnik załamania to wielkość
fizyczna
składająca
się z dwóch części: rzeczywistej - odpowiedzialnej za zjawisko
załamania
fali padającej na granicę dwóch ośrodków i urojonej -
która
odpowiada za
zjawisko absorpcji.
.
Współrzędna x-owa, (a) to część rzeczywista liczby zespolonej, natomiast
współrzędna
y-
owa -
b to jej część urojona. Analogicznie mówimy o
rzeczywistej
osi
0x
i osi urojonej 0y płaszczyzny 0xy.
W dalszym jednak ciągu przydatność liczb zespolonych była
mało
widoczna. Można ich było użyć
do
zgrabnego zapisu pewnych operacji na wektorach w przestrzeni
dwuwymiarowej na płaszczyźnie.
Dopiero w drugiej połowie 19. wieku zaczęła się objawiać
potęga
algebry
liczb zespolonych, a zwłaszcza teorii funkcji zmiennej zespolonej.
W
fizyce wielkości zespolone mają często znakomitą
interpretację
formalną -
np. zespolony współczynnik załamania to wielkość
fizyczna
składająca
się z dwóch części: rzeczywistej - odpowiedzialnej za zjawisko
załamania
fali padającej na granicę dwóch ośrodków i urojonej -
która
odpowiada za
zjawisko absorpcji.




Next: Magia i mistyka liczb;
Up: Kilka drobiazgów z historii
Previous: Pierre Fermat
Andrzej Lenda
1999-03-08
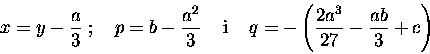
![\begin{displaymath}y = \sqrt[3] { \frac q 2 + \sqrt{\frac{q^2}{4} - \frac{p^3}{2...
...qrt[3] { \frac q 2 - \sqrt{\frac{q^2}{4} - \frac{p^3}{27} } }. \end{displaymath}](img31.gif)
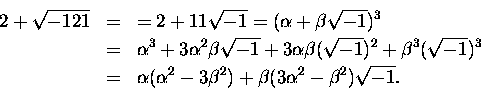
![\begin{eqnarray*}x & = & \sqrt[3]{2 + \sqrt{-121} } + \sqrt[3] {2 - \sqrt{-121} ...
...\\
& = & (2 + 1\times \sqrt{-1}) +(2 - 1\times \sqrt{-1}) = 4.
\end{eqnarray*}](img43.gif)
