
Linie regresji II rodzaju
Dwuwymiarowa zmienna losowa
Linie regresji I rodzaju z punktu widzenia fizyki są stosunkowo mało interesujące. Zamieściłem je w WVS dla kompletności wykładu. Linie regresji II rodzaju są natomiast niezwykle pożyteczne i na pewno każdy będzie je wielokrotnie wykorzystywał. Choćby na studenckiej pracowni I i II stopnia. Sądzę, że typowy student w ciągu pięciu lat studiów na naszym Wydziale musi policzyć prostą regresji II rodzaju co najmniej kilkadziesiąt razy. To chyba dostateczny powód, żeby dobrze zrozumieć o co w tym wszystkim chodzi. A poza tym to nie jest trudne!
| Załóżmy, że wielkość Y zależy liniowo od wielkości X. Wykonaliśmy kilka
pomiarów wielkości Y dla kilku różnych wartości X. Oczywiście na skutek błędów pomiaru lub też
statystycznego charakteru samego zjawiska punkty będące wynikiem pomiaru rzadko kiedy ułożą
się dokładnie na lini prostej. Wielkością Y może być na przykład napięcie mierzone na pewnym oporze, zaś wielkością X prąd płynący przez ten opór. | 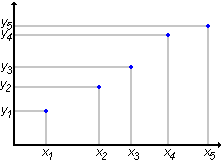 |
| Gdybyśmy wielokrotnie powtórzyli pomiar wielkości Y dla tej samej ustalonej wartości X=x to oczywiście wyniki Y będą rozrzucone wokół pewnej wartości najczęściej występującej. Na wykresie zależności Y od X możemy to przedstawić jako odcinki, których środki odpowiadają wartości najczęściej występującej, zaś szerokość w pewien sposób określa rozrzut otrzymanych wyników (często jako miarę tego rozrzutu stosuje się odchylenie standartowe). | 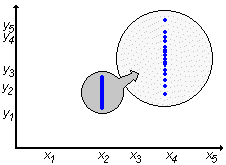 |
| Oczywiście dla każdej ustalonej wartości X=xi otrzymamy pewien rozrzut mierzonych wartości Y. Wykonując więc pojedyncze pomiary Y dla różnych X musimy pamiętać, że każda zmierzona wartość yi jest liczbą losową podlegającą rozkładowi zmiennej losowej Y. Wiemy, że teoretyczna zależność Y(X) jest liniowa, a więc powinna zachodzić zależność: yi = a xi + b. Naszym celem jest znalezienie współczynników a i b prostej, która najlepiej pasuje do zmierzonych punktów. | 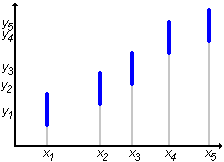 |
| Niestety przez odcinki odpowiadające wynikom naszych pomiarów można poprowadzić wiele prostych o różnych parametrach. Musimy więc znaleźć metodę, która pozwoli spośród nich wybrać taką prostą, która najlepiej odpowiada punktom pomiarowym. Regresja liniowa omówiona poniżej bazuje na tzw. metodzie najmniejszych kwadratów. | 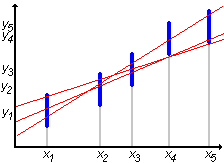 |
| Idea metody najmniejszych kwadratów jest bardzo prosta. Dla każdego pomiaru ustalamy "odległość" (liczoną wzdłuż osi y) odpowiadającego mu punktu pomiarowego od teoretycznej prostej o nieznanych partametrach a i b. Obliczamy sumę kwadratów tych odległości, a następnie szukamy takich wartości parametrów a i b, żeby suma ta była jak najmniejsza. Zakładamy, że prosta znaleziona w ten sposób jest najlepiej dopasowana do zmierzonych punktów. | 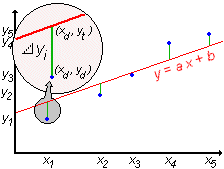 |
Jak znaleźć parametry a i b
Jak powiedziano powyżej zaczynamy od znalezienia odległości punktów pomiarowych od prostej. Ponieważ punkt doświadczalnie zmierzony (xd , yd) i odpowiadający mu punkt teoretyczny (xt , yt) mają te same współrzędne x to odległość między nimi będzie równa różnicy ich współrzędnych y. A ponieważ punkty na prostej teoretycznej spełniają równanie tej prostej więc możemy zapisać: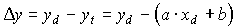
Zgodnie z następnym żądaniem, poszukujemy takich wartości parametrów prostej a i b, aby suma kwadratów tych różnic była jak najmniejsza:
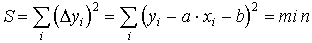
A powyższe zachodzi tylko wtedy, gdy pochodne z sumy kwadratów policzone względem parametru a i parametru b równają się zeru.
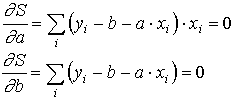
Otrzymujemy więc dwa równania i dwie niewiadome. Rozwiązaniem tych równań jest:
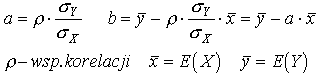
Tak więc, aby znaleźć prostą najlepiej dopasowaną do szeregu punktów pomiarowych należy obliczyć na podstawie zmierzonych wartości wartość oczekiwaną X (średnią), wartość oczekiwaną zmiennej Y, odchylenia standartowe obydwu zmiennych i współczynnik korelacji. Wielkości te wystarczy podstawić do wzorów na współczynniki a i b i już mamy prostą najlepiej dopasowaną do zmierzonych punktów.
Prostą najelpiej dopasowaną do zadanych punktów, wyznaczoną w opisany powyżej sposób metodą najmniejszych kwadratów o równaniu:
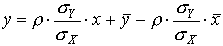
nazywamy prostą regresji II rodzaju zmiennej Y względem zmiennej X.
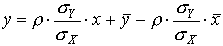
nazywamy prostą regresji II rodzaju zmiennej Y względem zmiennej X.
Prostą o równaniu:
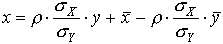
nazywamy prostą regresji II rodzaju zmiennej X względem zmiennej Y.
Pomiar oporu elektrycznego
W praktyce zazwyczaj korzystamy, jak w powyższych przykładach, z gotowych wzorów. Czasami
jednak, kiedy spotykamy się z zależnością nieliniową, chcąc znaleźć parametry takiej zależności
musimy w sposób jawny zastosować metodę najmniejszych kwadratów i wyliczyć wyrażenia na
konkretne parametry. Przykład takiego postępowania zawiera poniższe zadanie.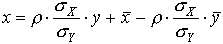
nazywamy prostą regresji II rodzaju zmiennej X względem zmiennej Y.
Zależność oporu od temperatury
Linearyzacja funkcji
W przypadku niektórych zależności nieliniowych zamiast poszukiwać parametrów takich funkcji, łatwiej jest je sprowadzić do postaci liniowej (zlinearyzować), następnie zastosować regresję liniową, a następnie powrócić do pierwotnej formy funkcji.
Funkcja wykładnicza
W przypadku niektórych zależności nieliniowych zamiast poszukiwać parametrów takich funkcji, łatwiej jest je sprowadzić do postaci liniowej (zlinearyzować), następnie zastosować regresję liniową, a następnie powrócić do pierwotnej formy funkcji.
| funkcja pierwotna | funkcja zlinearyzowana |
|---|---|
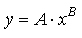 |  |
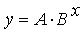 | 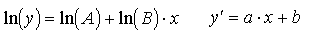 |
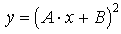 |  |
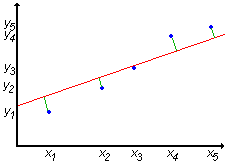 Warto zwrócić uwagę, że w
rozważaniach dotyczących lini regresji II rodzaju zakładaliśmy, że wartości zmiennej losowej X są
wyznaczone dokładnie, bez żadnego rozrzutu. Przy takim założeniu odległość punktu od prostej
liczyliśmy jako różnicę wartości zmiennej Y wyliczonej teoretycznie i zmierzonej doświadczalnie.
Jeżeli jednak zmienna X też podlega pewnym rozrzutom, to wówczas odległość punktów od prostej
powinniśmy wznaczać jako długość odcinka łączącego punkt z prostą i do tej prostej
prostopadłego. Jest to jednak dużo bardziej skomplikowane rozwiązanie i nie będziemy go tu
omawiać (przynajmniej w tym roku ;-) ). W praktyce najczęsciej ustalamy wartości zmiennej X i
traktujemy je jako dużo bardziej dokładne, niż wyniki pomiaru Y. Nie zawsze jednak tak być musi i trzeba sobie z tego zdawać
sprawę.
Warto zwrócić uwagę, że w
rozważaniach dotyczących lini regresji II rodzaju zakładaliśmy, że wartości zmiennej losowej X są
wyznaczone dokładnie, bez żadnego rozrzutu. Przy takim założeniu odległość punktu od prostej
liczyliśmy jako różnicę wartości zmiennej Y wyliczonej teoretycznie i zmierzonej doświadczalnie.
Jeżeli jednak zmienna X też podlega pewnym rozrzutom, to wówczas odległość punktów od prostej
powinniśmy wznaczać jako długość odcinka łączącego punkt z prostą i do tej prostej
prostopadłego. Jest to jednak dużo bardziej skomplikowane rozwiązanie i nie będziemy go tu
omawiać (przynajmniej w tym roku ;-) ). W praktyce najczęsciej ustalamy wartości zmiennej X i
traktujemy je jako dużo bardziej dokładne, niż wyniki pomiaru Y. Nie zawsze jednak tak być musi i trzeba sobie z tego zdawać
sprawę.