
Igła Buffona*
Wyobraźmy sobie następujące doświadczenie: rzucamy z pewnej wysokości igłę (patyk) o długości d na kartkę papieru, na której wymalowano linie równoległe odległe o 2d od siebie. Zadajmy pytanie: jakie jest prawdopodobieństwo, że patyk upadnie na papier w taki sposób, że przetnie jedną z równoległych linii? Popatrzmy na rysunek.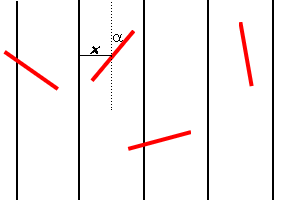
Położenie dowolnej igły rzuconej na papier możemy opisać podając dwie liczby:
x - odległość od umownie przyjętej linii zerowej
a - kąt jaki tworzy igła z kierunkiem lini
Zauważmy, że z racji symetrii wystarczy jeśli nasze rozważania ograniczymy do obszaru:
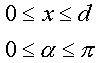
każda z wartości x i a z podanych przedziałów może wystąpić z równym prawdopodobieństwem. Możemy więc powiedzieć, że nasze doświadczenie sprowadza się do losowego wyboru punktu na płaszczyźnie w obszarze ograniczonym podanymi warunkami. Patrząc na poprzedni rysunek łatwo sformułować warunek jaki musi być spełniony, aby igła przecięła się z jedną z linii:
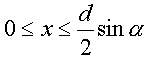
Graficznie warunek ten możemy zinterpretować następująco. Każdy punkt obszaru S (zakreskowany pionowo) odpowiada jakiejś pozycji rzuconej igły. Punkty w obszarze S1 (zakreskowanym poziomo) odpowiadają położeniom, w których igła przecina się z prostą.
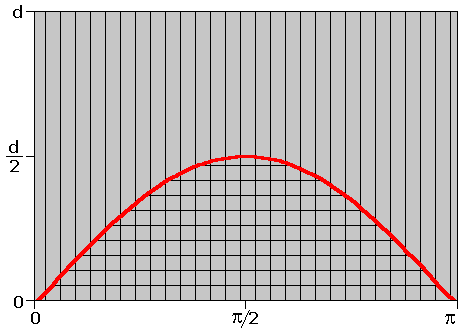
Ponieważ każdy punkt jest równie prawdopodobny możemy więc zapisać, że prawdopodobieństwo tego, że igła przetnie prostą jest równe:
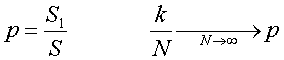
gdzie N jest liczbą rzuconych igieł, a k liczbą igieł, które przecięły proste. Policzmy pola S i S1:
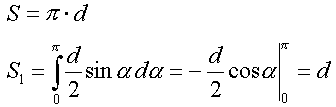
Teoretycznie wyliczone prawdopodobieństwo przecięcia prostej igłą jest bezpośrednio związane z liczbą p:
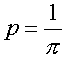
Wystarczy więc rzucić dużą liczbę igieł na papier z liniami, usunąć te, które linii nie przecięły i policzyć odpowiedni stosunek:
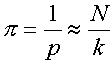
Jeśli jeszcze taki eksperyment powtórzymy wielokrotnie, możemy uzyskać zupełnie niezłe przybliżenie liczby pi. Do tego właśnie służy przedstawiony poniżej program.
Po uruchomieniu programu "PI" na ekranie pojawi się poniższe okno:

OBSŁUGA PROGRAMU
| suwakiem ustalasz liczbę igieł jakie mają być rozrzucone |  |
| przyciskiem uruchamiasz rozrzucenie igieł |  |
| na ekranie zobaczysz efekt |  |
| przyciskiem usuwasz igły, które nie przecięły się z liniami |  |
| na ekranie zobaczysz efekt |  |
| poniżej zostanie wyliczona wartość liczby p | 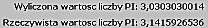 |
Spróbuj wykonać poniższe ćwiczenie.
Dla ustalonej liczby igieł N wykonaj k=10 losowań policz średnią wartość liczby p oraz jej odchylenie standartowe. Następnie powtórz te same rachunki dla k=50 i k=100.
Wykonaj ten sam test dla różnych wartości N (np. 100, 1000 i 10000). Co powiesz o otrzymanych wynikach w języku teorii estymacji?
PI
* Po raz pierwszy rozważania te przedstawił w 1777 roku G.L.Buffon. Stąd nazwa problemu.