idż do fizyka kwantowa. 2. Definicja i własności temperatury bezwzględnej; temperatura układów w równowadze cieplnej; pomiar temperatury. 3. Entropia (definicja mikroskopowa, małe przekazy ciepła); stan równowagi. 4. Układ kontaktujący się termicznie ze zbiornikiem ciepła (rozkład kanoniczny). 5. Paramagnetyzm (prawo Curie). Ciepło właściwe oscylatora harmonicznego. 6. Średnia energia i średnie ciśnienie gazu doskonałego. 7. Twierdzenie o wiriale w zastosowaniu do gazu doskonałego. Gazy rzeczywiste. 8. Ogólne równanie stanu gazów doskonałych. 9. Twierdzenie o ekwipartycji energii (wyprowadzenie i przykłady). 10. Maxwellowski rozkład prędkości. 11. Entropia gazu doskonałego; równanie adiabaty. 12. Zasady termodynamiki i związki statystyczne. Sprawność silnika. Cykl Carnota. 13. Potencjały termodynamiczne (wyprowadzenia) i tożsamości Maxwella. 14. Prawo Steana-Boltzmana. Prawo Wina. 15. Stan równowagi pomiędzy fazami; równanie Clausiusa - Clapeyrona. 16. Układy otwarte. Statystyki kwantowe. Granica klasyczna. 17. Rozkład Plancka. 18. Gęstość stanów w przestrzeniach 1, 2, 3-wymiarowych. Periodyczne a sztywne warunki brzegowe. 19. Gaz elektronów swobodnych. 20. Półprzewodniki: gęstość nośników, prawo działania mas, potencjał chemiczny. |
Opracowali: J. Ropka, B. Wróbel. Konsultacje: J. Wolny 1. Rozkład dwumienny; przykłady. Liczba stanów dozwolonych dla układu makroskopowego.Kiedy mamy do czynienia z dużą ilością obiektów, traktujemy je jako zespół
statystyczny, do którego stosujemy pojęcia prawdopodobieństwa. Zespół
statystyczny składa się z bardzo dużej liczby N układów "podobnych" do siebie.
Jeżeli pewien określony wynik doświadczenia oznaczony został wskaźnikiem r i
spośród N układów zespołu wynik ten uzyskany został na Nr układach, wówczas
iloraz 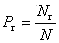 nazywamy prawdopodobieństwem wystąpienia wyniku r. Stosunek ten jest słuszny dla Należy wprowadzić warunek normalizujący: oraz podstawowe prawa rachunku prawdopodobieństwa: 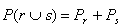 oraz
oraz Zespół statystyczny, którego obiekty mogą znajdować się w jednym z dwóch stanów z prawdopodobieństwami p i q (p+q=1) opisuje ROZKŁAD DWUMIENNY o rozkładzie prawdopodobieństwa: 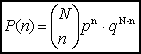 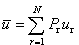 Ma ona bardzo proste własności. Jeżeli f(u) i g(u) są dowolnymi dwiema funkcjami zmiennej u to: 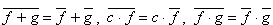 (ten ostatni związek obowiązuje dla zmiennych nie skorelowanych). Wartość średnia
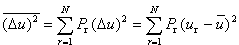 nazywamy wariancją zmiennej u. Wariancja może stać się równa zeru tylko wtedy, gdy wszystkie wartości ur
równe będą wartości średniej
Miarą liniową rozrzutu wielkości u jest pierwiastek kwadratowy z wariancji,, czyli tzw. odchylenie standardowe:
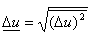
Przykłady zastosowania rozkładu dwumiennegoPrzykład 1Rozważmy idealny układ N cząstek o spinie połówkowym, które są statystycznie niezależne. Przyjmujemy
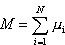 Obliczamy wartość średnią: 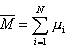 Prawdopodobieństwo, że jakiś dowolny moment magnetyczny ma określoną orientację, jest dla wszystkich momentów takie samo, a zatem dla każdej cząstki średni moment magnetyczny jest taki sam (tzn: 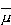 1 = 1 = 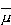 2 = K = 2 = K = 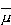 N
) i można go oznaczyć po prostu przez N
) i można go oznaczyć po prostu przez
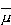 .
A zatem: .
A zatem:
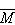 =N =N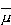 .
Obliczamy teraz wariancję M, tzn. wielkość .
Obliczamy teraz wariancję M, tzn. wielkość
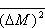 ,
gdzie ,
gdzie
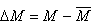 ,
a ,
a
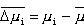 . .
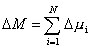 Aby znaleźć ( 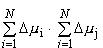 a więc: 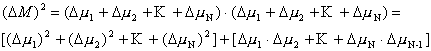 czyli: 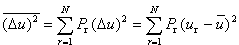 Pierwsza suma daje wszystkie człony kwadratowe otrzymane z pomnożenia przez
siebie tych samych wyrazów sumy. Suma podwójna zaś daje wszystkie iloczyny różniących
się od siebie składników sumy. Każdy z tych iloczynów jest średnio równy zeru,
jako że jest on równie często dodatni jak i ujemny. A zatem wzór zredukuje się
do zwykłej sumy wyrazów kwadratowych : 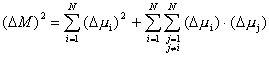 Prawdopodobieństwo, że dowolny moment ma jakąś określoną orientację jest dla każdego z momentów takie samo. Stąd wariancja 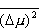 będzie taka sama dla każdej cząstki i można ją oznaczyć przez
będzie taka sama dla każdej cząstki i można ją oznaczyć przez
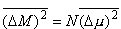 Odchylenie standardowe: 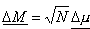
Z powyższych wzorów wynika, w jaki sposób
Przykład 2Rozważmy układ spinów w polu magnetycznym, które wyróżnia kierunek "do góry"
z prawdopodobieństwem p=0.51, więc q=0.49. Oznaczamy momenty ustawione "w górę"
Pole magnetyczne, w którym znajduje się układ, jest słabe (np. pole ziemskie), odpowiadające wartościom prawdopodobieństw p=0.51 i q=0.49. Podstawiając wartości i otrzymamy średni całkowity moment magnetyczny układu N cząsteczek 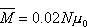 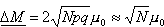 A zatem 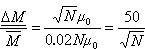
Rozważmy najpierw przypadek, w którym całkowita liczba cząsteczek jest stosunkowo niewielka, np. N=100, co daje
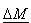 > >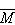 Rozrzut możliwych wartości M jest w takim przypadku bardzo duży.
Jeżeli natomiast rozważymy układ o rozmiarach makroskopowych, w którym liczba cząstek jest rzędu liczby Avogadro N=1024, to
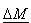 << <<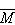 Rozrzut możliwych wartości M jest wówczas bardzo mały w stosunku do wielkości średniego całkowitego momentu magnetycznego układu 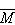 .
Gdybyśmy rozpoczęli robić pomiary wielkości M, to otrzymalibyśmy niemal zawsze wartości bardzo bliskie .
Gdybyśmy rozpoczęli robić pomiary wielkości M, to otrzymalibyśmy niemal zawsze wartości bardzo bliskie
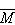 .
Dopóki stosowana przez nas metoda pomiaru nie byłaby wystarczająco dokładna, aby wykryć różnice momentu magnetycznego mniejsze niż 10-8 %, otrzymywalibyśmy właściwie zawsze wartość równą .
Dopóki stosowana przez nas metoda pomiaru nie byłaby wystarczająco dokładna, aby wykryć różnice momentu magnetycznego mniejsze niż 10-8 %, otrzymywalibyśmy właściwie zawsze wartość równą
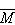 ,
nie zdając sobie sprawy z istnienia fluktuacji wokół tej wartości. ,
nie zdając sobie sprawy z istnienia fluktuacji wokół tej wartości.
RYSUNEK Przykład 3Interesuje nas rozmieszczenie cząsteczek w gazie. W naczyniu o objętości V0 znajduje się gaz doskonały złożony z N cząsteczek. Jeżeli gaz znajduje się w stanie równowagi, to prawdopodobieństwo p znalezienia się jakiejś cząsteczki w objętości V wynosi
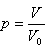 , , 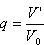 , ,Obliczamy wartość średnią 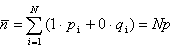 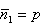 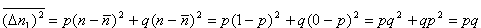 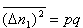 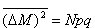 dla N cząstek. Odchylenie standardowe: 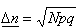 Błąd względny 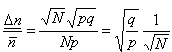
Dla ustalonych prawdopodobieństw p i q błąd względny maleje ze wzrostem liczby cząstek N, jak
Liczba stanów dozwolonych dla układu makroskopowego
Załóżmy, że mamy do czynienia z układem makroskopowym, dla którego dane są parametry zewnętrzne wyznaczające poziomy energetyczne układu. Całkowitą energię układu oznaczymy przez E. Aby ułatwić policzenie stanów, zgrupujemy je według energii, dzieląc obszar energii na równe małe przedziały o stałej odległości
Względna zmiana wielkości
W takim przypadku, liczby stanów o energiach znajdujących się pomiędzy E i E+
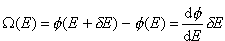 Przykład 1W jaki sposób obliczyć można liczbę stanów
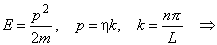 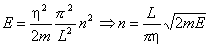 Ponieważ kolejne stany kwantowe odpowiadają wartościom n różniącym się o jeden, więc 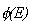 - czyli całkowita liczba stanów kwantowych o energiach mniejszych od E, a więc o liczbach kwantowych mniejszych od n, jest po prostu równa
- czyli całkowita liczba stanów kwantowych o energiach mniejszych od E, a więc o liczbach kwantowych mniejszych od n, jest po prostu równa
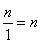 Stąd 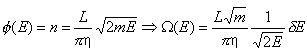 Przykład 2Załóżmy, że wewnątrz trójwymiarowego pudła (sześcianu o krawędzi L) porusza się swobodnie cząstka o masie m. Przyjmujemy, że Lx=Ly=Lz=L. Zatem
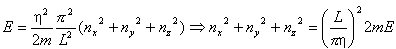 Dla zadanej wartości E, wartości nx, ny, nz spełniające to równanie, znajdują się na powierzchni kuli o promieniu R: 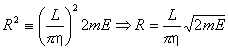 Liczba stanów 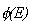 o energiach mniejszych od E jest równa objętości tej części kuli o promieniu R, dla której nx, ny, nz są dodatnie. o energiach mniejszych od E jest równa objętości tej części kuli o promieniu R, dla której nx, ny, nz są dodatnie.
Zatem 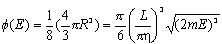 Liczba stanów o energiach znajdujących się pomiędzy E a E i E+ 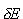 będzie wynosić:
będzie wynosić:

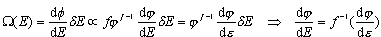
W miarę wzrostu energii E układu rośnie energia przypadająca na jeden stopień swobody. Odpowiednio też wzrasta stosunkowo powoli liczba stanów Liczba stanów dozwolonych
Otrzymać można następujące przybliżone wzory na zależność
 Dla każdego zwyczajnego układu zachodzi w przybliżeniu:
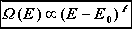 Możemy również znaleźć rząd wielkości : 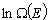
 Wielkości 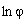 oraz oraz 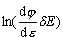 są dużo mniejsze od f, więc można je zaniedbać. są dużo mniejsze od f, więc można je zaniedbać.
Dla układu makroskopowego liczba stanów
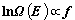 |
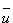 jest parametrem, który wskazuje
główną wartość, wokół której rozrzucone będą poszczególne wartości u. Byłoby
zatem pożyteczne wprowadzić jakiś parametr, który byłby miarą rozrzutu możliwych
wartości u dokoła wartości średniej
jest parametrem, który wskazuje
główną wartość, wokół której rozrzucone będą poszczególne wartości u. Byłoby
zatem pożyteczne wprowadzić jakiś parametr, który byłby miarą rozrzutu możliwych
wartości u dokoła wartości średniej 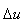 , (
, (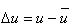 )
nie może być taką miarą, ponieważ
)
nie może być taką miarą, ponieważ  - składową momentu magnetycznego (wzdłuż kierunku "do góry") dla i-tego spinu. Interesuje nas całkowity moment magnetyczny M wzdłuż osi skierowanej "do góry":
- składową momentu magnetycznego (wzdłuż kierunku "do góry") dla i-tego spinu. Interesuje nas całkowity moment magnetyczny M wzdłuż osi skierowanej "do góry":
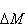 )2, musimy pomnożyć
przez siebie sumę
)2, musimy pomnożyć
przez siebie sumę 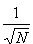 ,
czyli maleje z rosnącym N.
,
czyli maleje z rosnącym N.
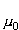 , a w dół
, a w dół 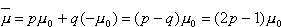 Wariancja momentu magnetycznego cząstki wynosi
Wariancja momentu magnetycznego cząstki wynosi 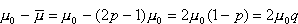 a także
a także 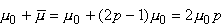 .
.
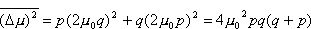 .
Ze względu na to, że p+q=1, otrzymujemy
.
Ze względu na to, że p+q=1, otrzymujemy
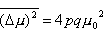 .
Ostatecznie
.
Ostatecznie
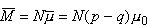 ,
oraz
,
oraz
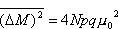 .
Odchylenie standardowe wielkości M wynosi:
.
Odchylenie standardowe wielkości M wynosi:
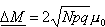 .
.
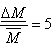 ,
czyli
,
czyli
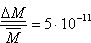 ,
czyli
,
czyli
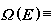 liczba stanów, których energie znajdują się w przedziale pomiędzy E i E+
liczba stanów, których energie znajdują się w przedziale pomiędzy E i E+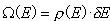 ,
gdzie
,
gdzie
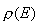 jest niezależne od wielości przedziału
jest niezależne od wielości przedziału
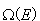 przy przejściu z jednego przedziału energii do sąsiedniego jest bardzo mała. Zatem
przy przejściu z jednego przedziału energii do sąsiedniego jest bardzo mała. Zatem 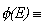 całkowita liczba stanów, których energie są mniejsze niż E.
całkowita liczba stanów, których energie są mniejsze niż E.
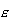 do całkowitej energii E układu. Przez
do całkowitej energii E układu. Przez 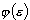 oznaczymy całkowitą liczbę możliwych wartości tej liczby kwantowej, dla których
związane z nimi przyczynki energii są mniejsze od
oznaczymy całkowitą liczbę możliwych wartości tej liczby kwantowej, dla których
związane z nimi przyczynki energii są mniejsze od 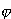 rośnie w przybliżeniu proporcjonalnie
do wielkości przedziału energii (
rośnie w przybliżeniu proporcjonalnie
do wielkości przedziału energii (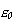 ). Możemy napisać:
). Możemy napisać: 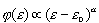 , gdzie
, gdzie 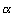 jest rzędu jedności.
jest rzędu jedności.
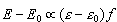 .
.
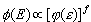 , gdzie
, gdzie 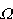 od E:
od E:
 E0
E0