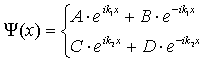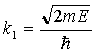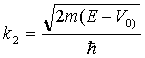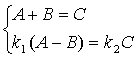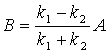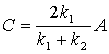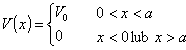idż do fizyka statystyczna.
1. Promieniowanie termiczne. Katastrofa w nadfiolecie.
2. Teoria Bohra układów wodoropodobnych.Doświadczenie Francka-Hertza.
3. Zjawisko fotoelektryczne. Wytwarzanie promieniowania rentgenowskiego.
4. Zjawisko Comptona.
5. Oddziaływanie promieniowania elektromagnetycznego z materią.
6. Fale de Broglie'a (własności, omówienie doświadczeń).
7. Postulaty fizyczne mechaniki kwantowej. Równanie Kleina - Gordona.
8. Mechanika falowa Schrödingera (operatory, postulaty).
9. Skok potencjału. Bariera potencjału. Zjawisko tunelowania.
10. Stany związane - nieskończona studnia potencjału.
11. Funkcje własne operatora pędu. Zasada nieoznaczoności.
12. Operator momentu pędu.
13. Równanie Schrödingera dla atomu wodoru; liczby kwantowe. Widma metali alkalicznych.
14. Orbitalny magnetyczny moment dipolowy. Precesja Larmora.
15. Oddziaływanie spin-orbita; sprzężenie L-S, j-j
16. Efekt Zeemana. Efekt Starka.
17. Konfiguracje elektronów w atomie. Reguły Hunda.
18. Liniowe widmo rentgenowskie. Prawo Moseley'a. Szerokość linii widmowej.
19. Atomy wieloelektronowe (helopodobne). Układ okresowy pierwiastków.
20. Molekuły dwuatomowe. Wiązania cząsteczkowe. Hybrydyzacja.
|
Notatki do wykładu z FIZYKI KWANTOWEJ.
Opracowali: J. Ropka, B. Wróbel.
Konsultacje: J. Wolny
9. Skok potencjału. Bariera potencjału. Zjawisko tunelowania.
Przedyskutujemy teraz rozwiązania
niezależnego od czasu równania Schrödingera dla cząstki, której
energię potencjalną można przedstawić w postaci funkcji V(x)
mającej różne stałe wartości na kilku kolejnych odcinkach osi x.
By rozwiązanie było fizycznie poprawne, funkcję
własną
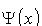 i ich pochodne i ich pochodne
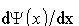 muszą mieć następujące własności: muszą mieć następujące własności:
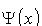 |
musi być skończona, |
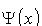 , , |
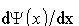 |
musi być jednoznaczna, |
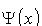 , , |
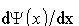 |
musi być ciągła. |
Warunki te zapewniają, że funkcje własne są
matematycznie "gładkimi" funkcjami, a więc i mierzalne
wielkości fizyczne obliczone na podstawie znajomości tych funkcji
własnych będą także zmieniać się w sposób gładki.
Skok potencjału
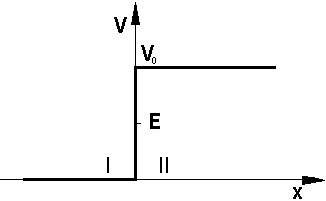
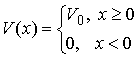
Warunki początkowe: cząsteczka nadlatuje z lewej
strony na barierę potencjału od której może się odbić lub wniknąć do
obszaru II
- E < V0
Załóżmy,
że cząstka o masie m i całkowitej energii E znajduje
się w obszarze x < 0 i porusza się w kierunku punktu, w
którym V(x) zmienia się skokowo. Według mechaniki
klasycznej cząstka będzie się poruszała swobodnie w tym obszarze do
chwili, gdy osiągnie punkt x = 0, w którym zadziała na nią
siła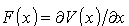 działająca w kierunku malejących x. Dalszy ruch cząsteczki
zależy, klasycznie biorąc, od związku między E i V0,
co jest również słuszne w mechanice kwantowej.
działająca w kierunku malejących x. Dalszy ruch cząsteczki
zależy, klasycznie biorąc, od związku między E i V0,
co jest również słuszne w mechanice kwantowej.
W celu kwantowego określenia ruchu naszej cząstki musimy znaleźć funkcję
falową, która będzie rozwiązaniem równania Schrödingera dla
potencjału schodkowego przy energii całkowitej E<V0.
Ponieważ mamy do czynienia z równaniem Schrödingera niezależnym
od czasu, problem nasz sprowadza się do rozwiązania go i znalezienia
funkcji własnych. Dla takiego potencjału oś x rozpada się na
dwa obszary. Równanie Schrödingera w każdym z tych obszarów
możemy zapisać:
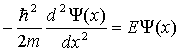 |
x<0 |
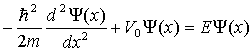 |
x>0 |
Te dwa równania rozwiązuje się oddzielnie. Wówczas funkcję własną
ważną dla całego obszaru x konstruuje się przez połączenie
razem w punkcie x = 0 tych dwóch rozwiązań w sposób
spełniający warunki, które wymagają, aby
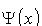 i i
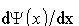 były wszędzie skończone i ciągłe.
były wszędzie skończone i ciągłe.
Rozwiązanie
pierwszego to:
Rozwiązanie
drugiego:
ale funkcja musi być ograniczona w 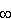 , więc C = 0. , więc C = 0.
| Wiemy, że |
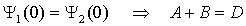 |
A - określa amplitudę fali padającej
B - amplituda fali odbitej od bariery
D - wiązka przepuszczona przez barierę
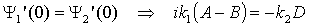
Rozwiązując ten układ równań
otrzymujemy :
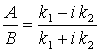 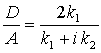
| Można obliczyć tzw. współczynnik
odbicia |
 . . |
Oznacza to, że fala zostanie odbita całkowicie, ale nie od krawędzi progu, tylko wniknie nieco w głąb.
| Oblicza się także tzw. współczynnik wnikania |
 |
którego niezerowa wartość oznacza, że cząsteczka wnika do bariery, a gęstość prawdopodobieństwa znalezienia cząsteczki w obszarze zabronionym maleje wykładniczo z x.
-
E > V0
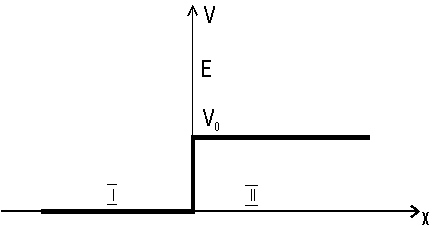
Całe rozumowanie przeprowadzamy
podobnie jak poprzednio.
Rozwiązanie:
Z warunków brzegowych przyjmujemy D=0 , gdyż w obszarze II fala nie ma od czego się odbić i porusza się tylko w prawo
Ponieważ 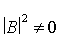 kwantowo istnieje nieznikająca wiązka odbita, mimo, iż klasycznie
cząsteczka w całości przechodzi do obszaru II. kwantowo istnieje nieznikająca wiązka odbita, mimo, iż klasycznie
cząsteczka w całości przechodzi do obszaru II.
Jeżeli E >>V0
to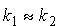 i
i
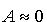 oraz oraz
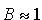 ,
co oznacza, że cząsteczka zachowuje się zgodnie z przewidywaniami
klasycznymi. ,
co oznacza, że cząsteczka zachowuje się zgodnie z przewidywaniami
klasycznymi.
Jeżeli jednak V0<0
i E0<<|V0|
(skok potencjału silnie ujemny) to k1 <<
k2 oraz
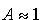 i i
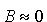 ;
następuje całkowite odbicie wiązki padającej (w przeciwieństwie do mechaniki klasycznej, która przewiduje całkowite przejście wiązki do obszaru II). Ten efekt kwantowy obserwuje się w fizyce jądrowej, np. wtedy, gdy padający neutron o niewielkiej energii ulega odbiciu napotykając silny potencjał przyciągający przy zbliżaniu się do powierzchni jądra. ;
następuje całkowite odbicie wiązki padającej (w przeciwieństwie do mechaniki klasycznej, która przewiduje całkowite przejście wiązki do obszaru II). Ten efekt kwantowy obserwuje się w fizyce jądrowej, np. wtedy, gdy padający neutron o niewielkiej energii ulega odbiciu napotykając silny potencjał przyciągający przy zbliżaniu się do powierzchni jądra.
Bariera potencjału
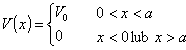
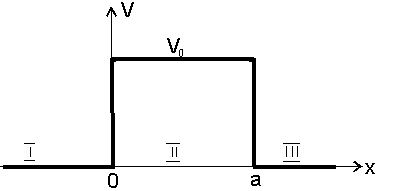
(cząsteczki nadlatują z lewej strony)
Rozwiązaniem równania Schrödingera (E<V0)
są w każdym z obszarów odpowiednie funkcje:
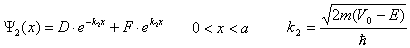

Należy zapisać warunki ciągłości na funkcje falową i jej pochodną w punktach x = 0 i x = a. Otrzymujemy cztery równania na współczynniki B, C, D, F wyrażone od amplitudy fali padającej A.
W przypadku bariery mamy do czynienia z ciekawym zjawiskiem - tunelowaniem. Polega ono na tym, że istnieje pewne niezerowe prawdopodobieństwo znalezienia cząstki po drugiej stronie bariery potencjału, mimo że E<V0. W rzeczywistości zjawisko tunelowania obserwowane jest w dobrze wszystkim znanym zjawisku: dwa skręcone druty przewodzą prąd pomimo, że na ich powierzchni często znajdują się tlenki i zabrudzenia, które są dobrymi izolatorami. Elektrony tunelują przez tę barierę i prąd może płynąć. Zjawisko tunelowania wykorzystano w tzw. diodach tunelowych. Zjawisko tunelowania obserwujemy również w czasie rozpadów promieniotwórczych.
góra
|
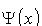
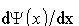

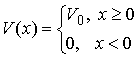
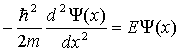
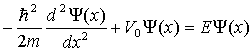
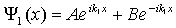

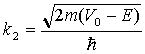
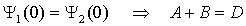
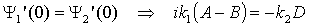
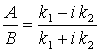
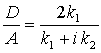
 .
.