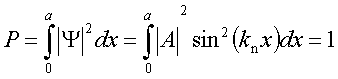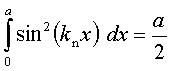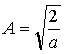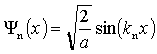idż do fizyka statystyczna. 2. Teoria Bohra układów wodoropodobnych.Doświadczenie Francka-Hertza. 3. Zjawisko fotoelektryczne. Wytwarzanie promieniowania rentgenowskiego. 4. Zjawisko Comptona. 5. Oddziaływanie promieniowania elektromagnetycznego z materią. 6. Fale de Broglie'a (własności, omówienie doświadczeń). 7. Postulaty fizyczne mechaniki kwantowej. Równanie Kleina - Gordona. 8. Mechanika falowa Schrödingera (operatory, postulaty). 9. Skok potencjału. Bariera potencjału. Zjawisko tunelowania. 10. Stany związane - nieskończona studnia potencjału. 11. Funkcje własne operatora pędu. Zasada nieoznaczoności. 12. Operator momentu pędu. 13. Równanie Schrödingera dla atomu wodoru; liczby kwantowe. Widma metali alkalicznych. 14. Orbitalny magnetyczny moment dipolowy. Precesja Larmora. 15. Oddziaływanie spin-orbita; sprzężenie L-S, j-j 16. Efekt Zeemana. Efekt Starka. 17. Konfiguracje elektronów w atomie. Reguły Hunda. 18. Liniowe widmo rentgenowskie. Prawo Moseley'a. Szerokość linii widmowej. 19. Atomy wieloelektronowe (helopodobne). Układ okresowy pierwiastków. 20. Molekuły dwuatomowe. Wiązania cząsteczkowe. Hybrydyzacja. |
Opracowali: J. Ropka, B. Wróbel. Konsultacje: J. Wolny 10. Stany związane - nieskończona studnia potencjału.Jeżeli energia cząsteczki nie pozwala jej na opuszczenie określonego obszaru powstają tzw. stany związane. Stan związany ma skwantowany wektor falowy k, tzn. tylko niektóre wartości wektora falowego są spełnione, ponieważ musi powstać fala, która ma węzły na barierach.
Potencjał nieskończenie głębokiej
prostokątnej studni ma tę własność, że wiąże cząstkę o skończonej
energii E Nieskończona studnia potencjału.
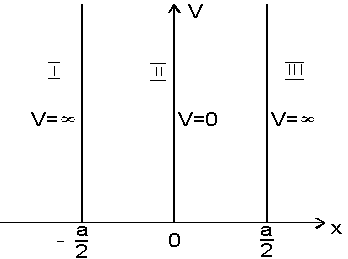
W obszarach I i III cząsteczka nie występuje i funkcja falowa zanika
Można też szukać rozwiązań postaci
(Uwaga: w przypadku nieskończonego skoku potencjału nie uciąglamy pochodnej funkcji falowej ). Oba te warunki muszą być spełnione, więc wybieramy taką wartość k, by
Ze związku
Dochodzimy więc do wniosku, że dozwolone są tylko pewne wartości energii całkowitej E, czyli że jest ona skwantowana.
Wnioskujemy więc, że istnienie energii drgań zerowych wynika z konieczności istnienia ruchu zerowego. Stoi to w sprzeczności z zasadami fizyki klasycznej. W analogiczny sposób można pokazać, że dla studni potencjału spełniającej warunek V(x)=0
dla 0
góra |
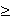 0. W
mechanice klasycznej dozwolona jest dowolna wartość energii,
natomiast w mechanice kwantowej dozwolone są tylko pewne dyskretne
wartości własne En. Dla niezbyt dużych wartości
liczby kwantowej n odpowiadające im wartości własne i funkcje
własne użyte być mogą jako przybliżenie odpowiadających im wartości
własnych i funkcji własnych dla potencjału o dużym, lecz skończonym
V0.
0. W
mechanice klasycznej dozwolona jest dowolna wartość energii,
natomiast w mechanice kwantowej dozwolone są tylko pewne dyskretne
wartości własne En. Dla niezbyt dużych wartości
liczby kwantowej n odpowiadające im wartości własne i funkcje
własne użyte być mogą jako przybliżenie odpowiadających im wartości
własnych i funkcji własnych dla potencjału o dużym, lecz skończonym
V0.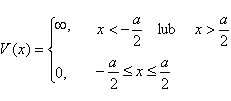
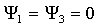
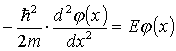
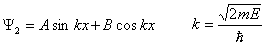
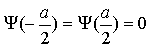
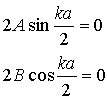
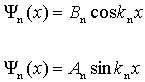
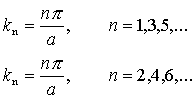
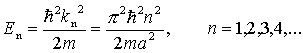
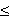 x
x