
Opis rozkładu
Jednowymiarowa zmienna losowa
Oczywiście najdokładniejszym i jednoznacznym sposobem opisu zmiennej losowej X jest podanie jej funkcji gęstości prawdopodobieństwa lub też dystrybuanty. Czasami nie interesuje nas jednak dokładny rozkład, a tylko pewne jego cechy. Na przykład na podstawie informacji o rorzucie dochodów różnych ludzi wokół średniej wartości dochodu w danym kraju czy firmie możemy wnioskować o stopniu rozwarstwienia zarobkowego. Poniżej przedstawiono dwa sposoby scharakteryzowania rozkładu zmiennej losowej poprzez tzw. momenty zmiennej losowej oraz poprzez parametry opisowe.
Momentem zwykłym rzędu k zmiennej losowej X nazywamy:
| dla zmiennej losowej dyskretnej | dla zmiennej losowej ciągłej | |
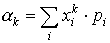 |
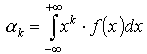 |
Momentem centralnym rzędu k zmiennej losowej X nazywamy:
| dla zmiennej losowej dyskretnej | dla zmiennej losowej ciągłej | |
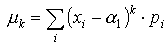 |
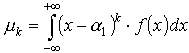 |
Charakterystyka rozkładu poprzez momenty zwykłe
Wartością oczekiwaną E(X)
(średnią*) zmiennej losowej X nazywamy:
Zauważmy, że E(X) nie jest zmienną losową.
E(X) ma konkretną, dokładnie określoną wartość liczbową - nie może więc być zmienną
losową.| dla zmiennej losowej dyskretnej | dla zmiennej losowej ciągłej | |
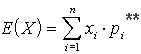 |
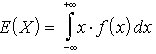 |
Wartość oczekiwaną dla dowolnej funkcji H (X) zmiennej losowej X obliczamy jako:
| dla zmiennej losowej dyskretnej | dla zmiennej losowej ciągłej | |
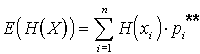 |
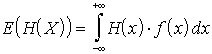 |
* Wartość oczekiwaną często - potocznie - nazywa się wartością średnią. Nie należy jej mylić ze średnią arytmetyczną. W całym Vademecum określenie średnia bez dopisku arytmetyczna będzie dotyczyć wartości oczekiwanej.
** W ogólności górna granica sumowania może być nieskończona (dla zmiennej o nieskończonym, przeliczalnym zbiorze wartości). W praktyce laboratoryjnej z taką sytuacją raczej się nie spotkamy.
Momenty zwykłe i momenty centralne rzędu k możemy oczywiście wyrazić poprzez wartość oczekiwaną odpowiedniej funkcji:
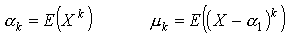
Charakterystyka rozkładu poprzez momenty centralne
Omówmy kilka pierwszych momentów centralnych.
 | Zerowy moment centralny |
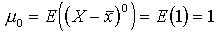 Moment ten jest zawsze równy jedności. Z punktu widzenia opisu rozkładu zmiennej losowej jest więc bezużyteczny. |
 | Pierwszy moment centralny |
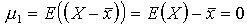 Moment ten jest zawsze równy zeru. Podobnie jak poprzednio ten moment również nie wnosi informacji na temat rozkładu zmiennej losowej. |
 | Drugi moment centralny |
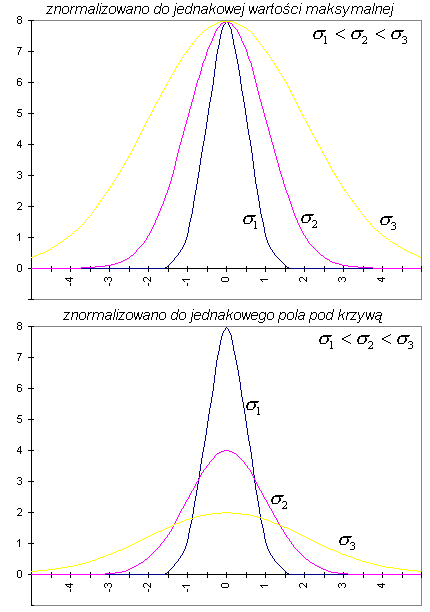
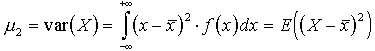 Moment ten jest jednym z ważniejszych w opisie rozkładu zmiennej losowej. Moment ten opisuje rozrzut wartości przyjmowanych przez zmienną losową wokół wartości średniej.
Drugi moment centralny nazywany jest wariancją. Mała wariancja oznacza, że wartości zmiennej losowej są
skupione wokół wartości średniej; duża zaś oznacza, że wartości zmiennej losowej są w dość dużym
zakresie "porozrzucane" wokół wartości średniej.
Często używanym parametrem opisującym rozkład jest odchylenie standardowe.
Odchyleniem standardowym
zmiennej losowej X nazywamy pierwiastek kwadratowy z wariancji i oznaczamy:
Podobnie jak wariancja, również odchylenie standardowe opisuje "szerokość" rozkładu. Jest
jednak wygodniejsze w użyciu
ponieważ, wyraża się w tych samych jednostkach co zmienna losowa X.
 |
 | Trzeci moment centralny |
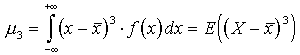 Moment ten opisuje stopień asymetrii rozkładu zmiennej losowej. Wartość tego moment jest jednak trudna w interpretacji, dlatego częściej stosuje się do opisu rozkładu współczynnik asymetrii.
Współczynnikiem asymetrii
(skośnością) rozkładu zmiennej losowej X nazywamy stosunek trzeciego momentu
centralnego do trzeciej potęgi odchylenia standadowego i oznaczamy:
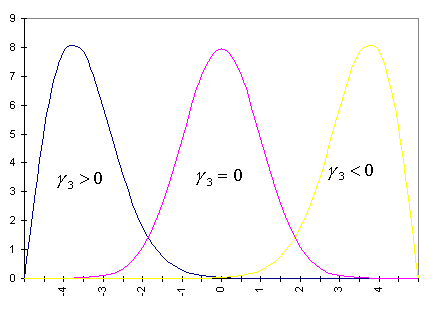
Współczynnik asymetrii opisuje stopień asymetrii rozkładu. Gdy g3>0
wówczas rozkład ma "ogon" rozwinięty w stonę dużych wartości x, natomiast gdy g3<0 wówczas rozkład
jest przesunięty w prawo, a ogon rozciąga się w stronę mniejszych x. Im g3
jest bliższe
zeru tym bardziej symetryczny jest rozkład.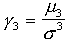
 |
 | Czwarty moment centralny |
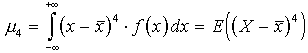 Moment ten informuje czy rozkład ma charakter smukłego, "ostrego" maksimum, czy też jest raczej płaski. Najczęściej zamiast czwartego momentu centralnego używa się tzw. współczynnika koncentracji.
Współczynnikiem koncentracji
(kurtozą) rozkładu zmiennej losowej X nazywamy stosunek czwartego momentu
centralnego do czwartej potęgi odchylenia standadowego i oznaczamy:
Chcąc odnieść omawianą cechę do specjalnego typu rozkładu zwanego rozkładem normalnym
stosujemy współczynnik spłaszczenia.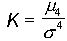
Współczynnikiem spłaszczenia
(ekscesem) rozkładu zmiennej losowej X nazywamy:
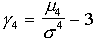 Eksces opisuje płaskość (czasami mówi się o "szczytowości") rozkładu. Eksces ujemny odpowiada mniejszemu wyostrzniu maksimów rozkładu w porównaniu z rozkładem normalnym. Eksces dodatni odpowiada większemu wyostrzeniu. 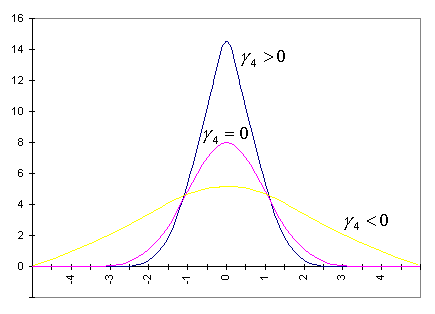
|
W omawianym w tej części WVS zagadnieniu istnieje spore zamieszanie terminologiczne. Wszystkie nazwy (kurtoza, skośność...) przyjęte w powyższych definicjach są zgodne z terminologią stosowaną w książce W. Krysicki ... "Rachunek
prawdopodobieństwa i statystyka ...", ale nie zawsze są zgodne z tym co można znaleźć w
innych podręcznikach,
a w szczególności nie są zgodne z nazwami funkcji statystycznych dostępnych w arkuszu
kalkulacyjnym EXCEL.
Własności wartości oczekiwanej i wariancji
Charakterystyka rozkładu poprzez parametry opisowe
Rozstępem zmiennej losowej X nazywamy różnicę pomiędzy największą a
najmniejszą wartością przyjmowaną przez zmienną losową:
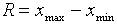
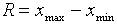
Jeżeli zmienna losowa może przyjmować wartości dążące do minus lub plus nieskończoności to ustalenie rozstępu jest nie możliwe.
Mediana x0.5 to taka wartość zmiennej losowej X, że
prawdopodobieństwo przyjęcia przez zmienną wartości mniejszych od x0.5 jest
równe 1/2. Oznacza to, że mediana "dzieli" rozkład prawdopodobieństwa na dwie połowy. W
przypadku zmiennej losowej ciągłej:
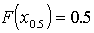
zaś w przypadku zmiennej losowej dyskretnej każda liczba x0.5 spełniająca poniższy warunek, będzie medianą rozkładu dyskretnego:
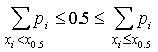
W USA podaje się nie tylko średnią płacę, ale również medianę.
Jeżeli słyszymy, że mediana wynosi 30tys. $ rocznie, a my zarabiamy 28tys. $ to od razu wiemy, że
znajdujemy się w tej połowie społeczeństwa, która zarabia poniżej 30tys. $. W
przeciwieństwie do średniej, mediana pozwala "umiejscowić" się nam na tle społeczeństwa.
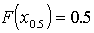
zaś w przypadku zmiennej losowej dyskretnej każda liczba x0.5 spełniająca poniższy warunek, będzie medianą rozkładu dyskretnego:
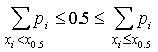
Kwantylem rzędu p nazywamy taką wartość zmiennej losowej X, że
prawdopodobieństwo przyjęcia przez zmienną wartości mniejszych od xp jest równe
właśnie p. W szczególności kwantyl x0.25 nazywamy pierwszym (albo dolnym) kwartylem, kwantyl
x0.5 jest po prostu medianą (ale nazywany też bywa drugim kwartylem), a x0.75 to oczywiście
trzeci (albo górny) kwartyl rozkładu zmiennej losowej X.
Modą albo wartością modalną xm rozkładu zmiennej losowej X
nazywamy wartość zmiennej losowej, dla której rozkład prawdopodobieństwa przyjmuje lokalne
maksimum.
Poniższe przykłady pokazują w jaki sposób wyznaczamy podstawowe charakterystyki dyskretnego i ciągłego rozkładu zmiennej losowej.
Wyniki kolokwium Ciągła zmienna losowa Średnia i wariancja